Graphing Absolute Value EquationsPage
1
1
Slide 1
Topic: Graphing Absolute Value Equations
Name: Date: Period:
Warm-Up:
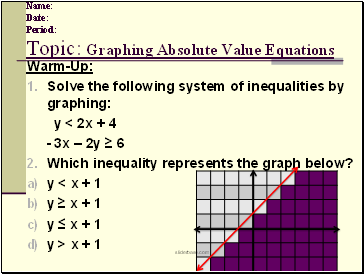
Solve the following system of inequalities by graphing:
y < 2x + 4
- 3x – 2y ≥ 6
Which inequality represents the graph below?
y < x + 1
y ≥ x + 1
y ≤ x + 1
y > x + 1
Slide 2
Home-Learning Assignment #5 Review
Slide 3
Quiz #8
Slide 4
Graphing Absolute Value Equations
How do I make one of those V graphs?
Slide 5
Absolute value transformation
Vocabulary:
Translation: shifts the parent function graph horizontally and vertically.
Reflection: it creates a mirror image of the parent-function graph across the line of reflection.
Slide 6
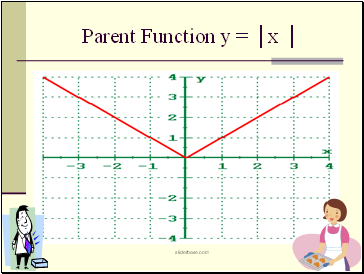
Parent Function y = │x │
Slide 7
Vertical Movements?
Absolute value rules:
If you have minus outside the absolute value, you move down on the coordinate plane.
y =│x│- 2
If you have addition outside the absolute value, you move up on the coordinate plane.
y =│x│+ 2
Slide 8
Lets practice!
y = │x│ - 4
y = │x│+ 3
Slide 9
Your turn!
y = │x│ + 7
y = │x│ - 2
Slide 10
Horizontal Movements?
Absolute value special rules:
If you have minus inside the absolute value, you move to the right on the coordinate plane.
y =│x - 2 │
If you have addition inside the absolute value, you move to the left on the coordinate plane.
y =│x + 2 │
Slide 11
Lets Practice!
y =│x - 5│
y =│x + 6│
Slide 12
Your Turn!
y =│x + 4│
y =│x - 1│
Slide 13
What about y = │x - 4 │+ 5
Slide 14
1 2
Contents
- Topic: Graphing Absolute Value Equations
- Graphing Absolute Value Equations
- Absolute value transformation
- Vertical Movements?
- Horizontal Movements?
- Verbal Comprehension Analysis
- Wrap-up
Last added presentations
- Madame Marie Curie
- Health Physics
- Static and Kinetic Friction
- Radiation
- Direct heat utilization of geothermal energy
- Mechanical, Electromagnetic, Electrical, Chemical and Thermal
- Upcoming Classes