Design Realization lecture 25

Page
2

Refractive index

High-quality optical glass is engineered to have a constant refractive index across the visible spectrum.

Deviations are still possible. Such deviations are called chromatic aberration.

Slide 13

Refractive indices

Water is approximately 1.33

Normal glass and acrylic plastic is about 1.5

Polycarbonate is about 1.56

Highest optical plastic index is 1.66

Bismuth glass is over 2

Diamond is 2.42

Slide 14

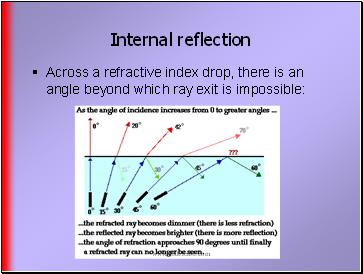
Internal reflection

Across a refractive index drop, there is an angle beyond which ray exit is impossible:

Slide 15

Total internal reflection (TIR)

The critical angle is where the refracted ray would have 90 incidence.

The internal reflection angle is therefore:

For glass/acrylic, this is 42

For diamond, it is 24 - light will make many internal reflections before leaving, creating the “fire” in the diamond.

Slide 16

Penta-prisms

Penta-prisms are used in SLR cameras to rotate an image without inverting it.

They are equivalent to two conventional mirrors, and cause a 90 rotation of the image, without inversion.

An even number of mirrors produce a non- inverted rotated image of the object.

Slide 17

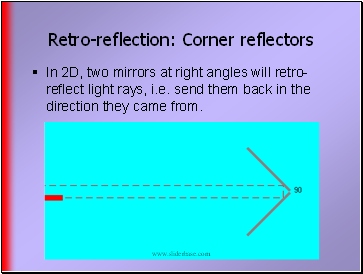
Retro-reflection: Corner reflectors

In 2D, two mirrors at right angles will retro-reflect light rays, i.e. send them back in the direction they came from.

Slide 18

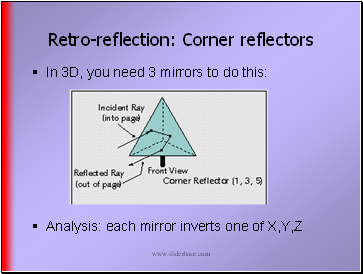
Retro-reflection: Corner reflectors

In 3D, you need 3 mirrors to do this:

Analysis: each mirror inverts one of X,Y,Z

Slide 19

Retro-reflection: TIR spheres

Consider a sphere and an incoming ray.

Incoming and refracted ray angles are , .

For the ray to hit the centerline,  = 2.

For retro-reflection, we want  = sin  /sin 

For small angles,  = 2 gives good results.

Slide 20

Retro-reflective sheets

Inexpensive retro-reflective tapes are available that use tiny corner reflectors or spheres embedded in clear plastic (3M Scotchlite)

They come in many colors, including black.

Slide 21