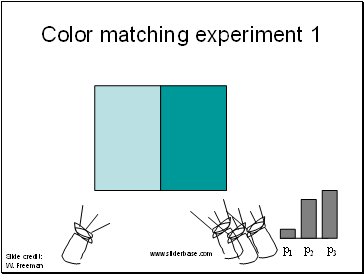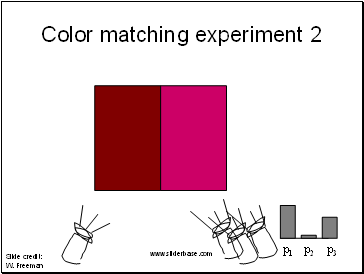Color

Page
3

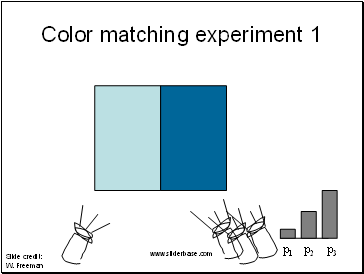
Color matching experiment 1

Slide credit: W. Freeman

Slide 22

Color matching experiment 1

p1 p2 p3

Slide credit: W. Freeman

Slide 23

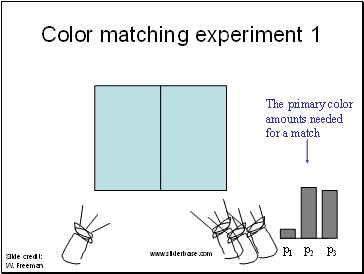
Color matching experiment 1

p1 p2 p3

Slide credit: W. Freeman

Slide 24

Color matching experiment 1

p1 p2 p3

Slide credit: W. Freeman

Slide 25

Color matching experiment 2

Slide credit: W. Freeman

Slide 26

Color matching experiment 2

p1 p2 p3

Slide credit: W. Freeman

Slide 27

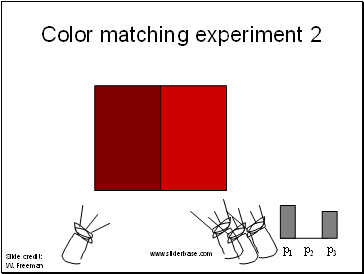
Color matching experiment 2

p1 p2 p3

Slide credit: W. Freeman

Slide 28

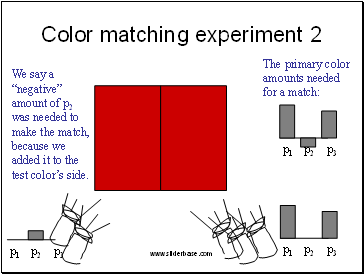
Color matching experiment 2

p1 p2 p3

p1 p2 p3

We say a “negative” amount of p2 was needed to make the match, because we added it to the test color’s side.

The primary color amounts needed for a match:

Slide 29

Color matching

What must we require of the primary lights chosen?

How are three numbers enough to represent entire spectrum?

Slide 30

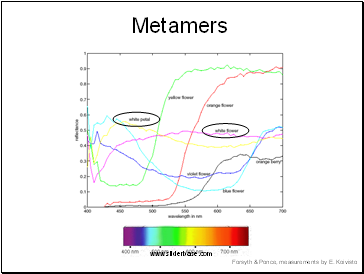
Metamers

If observer says a mixture is a match  receptor excitations of both stimuli must be equal.

But lights forming a perceptual match still may be physically different

Match light: must be combination of primaries

Test light: any light

Metamers: pairs of lights that match perceptually but not physically

Slide 31

Forsyth & Ponce, measurements by E. Koivisto

Metamers

Slide 32

Grassman’s laws

If two test lights can be matched with the same set of weights, then they match each other:

Suppose A = u1 P1 + u2 P2 + u3 P3 and B = u1 P1 + u2 P2 + u3 P3. Then A = B.

If we scale the test light, then the matches get scaled by the same amount:

Suppose A = u1 P1 + u2 P2 + u3 P3. Then kA = (ku1) P1 + (ku2) P2 + (ku3) P3.

If we mix two test lights, then mixing the matches will match the result (superposition):

Suppose A = u1 P1 + u2 P2 + u3 P3 and B = v1 P1 + v2 P2 + v3 P3. Then A+B = (u1+v1) P1 + (u2+v2) P2 + (u3+v3) P3.

Here “=“ means “matches”.