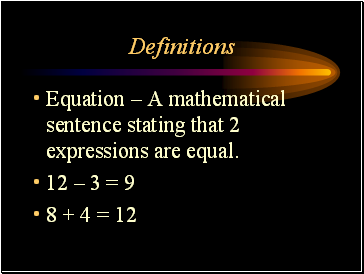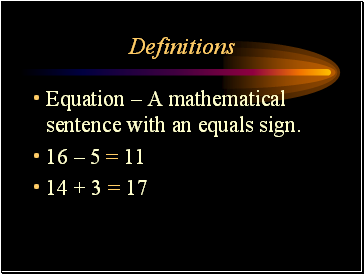Algebra II

Page
1

Slide 1

Algebra II

By Monica Yuskaitis

Slide 2

Definitions

Equation – A mathematical sentence stating that 2 expressions are equal.

12 – 3 = 9

8 + 4 = 12

Slide 3

Definitions

Equation – A mathematical sentence with an equals sign.

16 – 5 = 11

14 + 3 = 17

Slide 4

Definitions

Equals Sign (=) Means that the amount is the same on both sides.

4 + 2 = 6

5 – 2 = 3

Slide 5

An Equation is like a balance scale. Everything must be equal on both sides.

10

5 + 5

=

Slide 6

When the amounts are equal on both sides it is a true equation.

12

6 + 6

=

Slide 7

When the amounts are unequal on both sides it is a false equation.

8

2 + 2

=

Slide 8

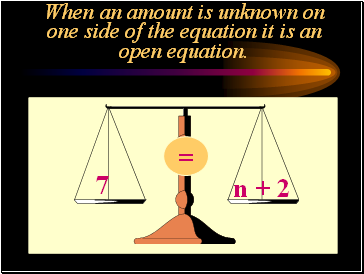
When an amount is unknown on one side of the equation it is an open equation.

7

n + 2

=

Slide 9

When you find a number for n you change the open equation to a true equation. You solve the equation.

7

n + 2

=

5

Slide 10

Are these equations true, false or open?

11 - 3 = 5

13 + 4 = 17

N + 4 = 7

12 – 3 = 8

3 + v = 13

15 – 6 = 9

false

true

open

false

open

true

Slide 11

Definitions

Inverse operation – the opposite operation used to undo the first.

4 + 3 = 7 7 – 4 = 3

6 x 6 = 36 36 / 6 = 6

Slide 12

How to solve an addition equation

Use the inverse operation for addition which is subtraction

m + 8 = 12 12 - 8 = 4

m = 4 4 + 8 = 12

Slide 13

How to solve a subtraction equation

Use the inverse operation for subtraction which is addition

m - 3 = 5 5 + 3 = 8

m = 8 8 - 3 = 5

Slide 14

Solve these equations using the inverse operations