Pythagoras Theorem

Page
1

Slide 1

THE

PYTHAGORAS'

THEOREM

Slide 2

Slide 3

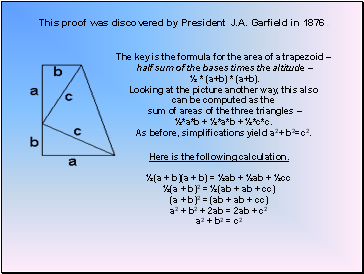
This proof was discovered by President J.A. Garfield in 1876 .

The key is the formula for the area of a trapezoid –

half sum of the bases times the altitude –

½ * (a+b) * (a+b).

Looking at the picture another way, this also

can be computed as the

sum of areas of the three triangles –

½*a*b + ½*a*b + ½*c*c.

As before, simplifications yield a2+ b2=c2.

Here is the following calculation.

½(a + b)(a + b) = ½ab + ½ab + ½cc

½(a + b)2 = ½(ab + ab + cc)

(a + b)2 = (ab + ab + cc)

a2 + b2 + 2ab = 2ab + c2

a2 + b2 = c2

Slide 4

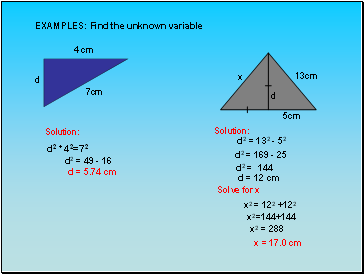
EXAMPLES: Find the unknown variable

4 cm

7cm

d

Solution:

d2 + 42=72

d2 = 49 - 16

d = 5.74 cm

d

x

13cm

5cm

Solution:

d2 = 132 - 52

d2 = 169 - 25

d2 = 144

d = 12 cm

Solve for x

x2 = 122 +122

x2=144+144

x2 = 288

x = 17.0 cm

Slide 5

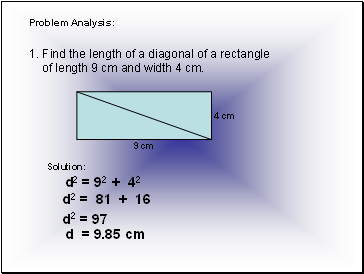
Problem Analysis

Find the length of a diagonal of a rectangle

of length 9 cm and width 4 cm.

4 cm

9 cm

Solution:

d2 = 92 + 42

d2 = 81 + 16

d2 = 97

d = 9.85 cm

Slide 6

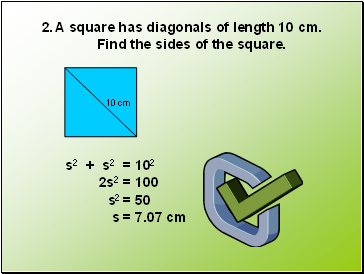
A square has diagonals of length 10 cm.

Find the sides of the square.

10 cm

s2 + s2 = 102

2s2 = 100

s2 = 50

s = 7.07 cm

Slide 7

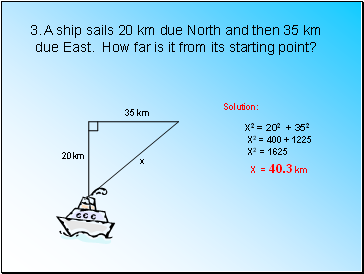
A ship sails 20 km due North and then 35 km

due East. How far is it from its starting point?

20km

35 km

x

Solution:

X2 = 202 + 352

X2 = 400 + 1225

X2 = 1625

X = 40.3 km

Slide 8

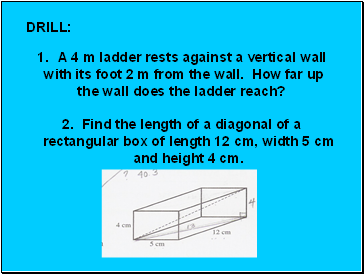
DRILL:

A 4 m ladder rests against a vertical wall

with its foot 2 m from the wall. How far up

the wall does the ladder reach?

2. Find the length of a diagonal of a rectangular box of length 12 cm, width 5 cm and height 4 cm.

Slide 9

“It is better wither to be silent, or to say things

of more value than silence.

Sooner throw a pearl at hazard

than an idle or useless word;

and do not say a little in many

words, but a great deal in a few. “

-Pythagoras

Slide 10