Right Prism volume

Page
1

Slide 1

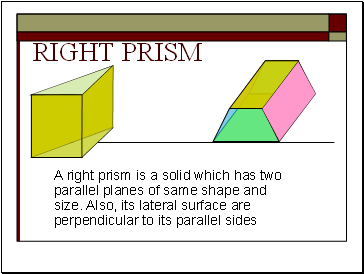
Right prism

A right prism is a solid which has two parallel planes of same shape and size. Also, its lateral surface are perpendicular to its parallel sides

Slide 2

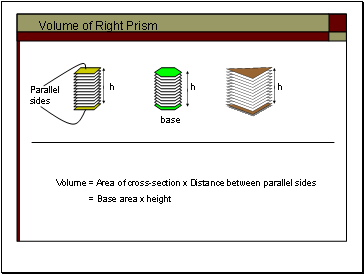
Volume of Right Prism

Volume = Area of cross-section x Distance between parallel sides

= Base area x height

h

h

h

Parallel sides

base

Slide 3

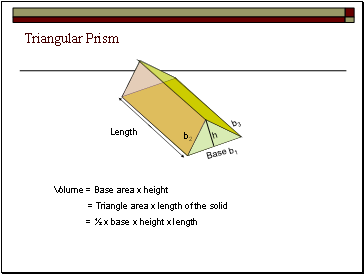
Triangular Prism

Volume = Base area x height

= Triangle area x length of the solid

= ½ x base x height x length

Length

Base

h

b2

b1

b3

Slide 4

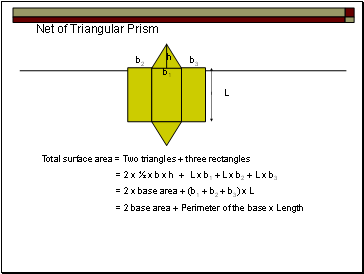
Net of Triangular Prism

Total surface area = Two triangles + three rectangles

= 2 x ½ x b x h + L x b1 + L x b2 + L x b3

= 2 x base area + (b1 + b2 + b3) x L

= 2 base area + Perimeter of the base x Length

L

b1

h

b2

b3

Slide 5

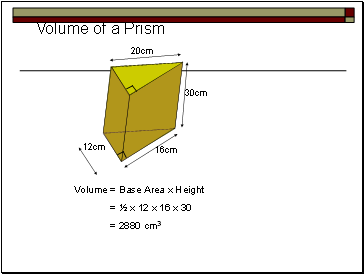
Volume of a Prism

16cm

12cm

20cm

30cm

Volume = Base Area x Height

= ½ x 12 x 16 x 30

= 2880 cm3

Slide 6

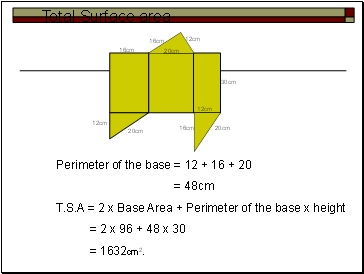
Total Surface area

Perimeter of the base = 12 + 16 + 20

= 48cm

T.S.A = 2 x Base Area + Perimeter of the base x height

= 2 x 96 + 48 x 30

= 1632cm2.

30cm

20cm

12cm

16cm

12cm

20cm

16cm

12cm

20cm

16cm

Slide 7

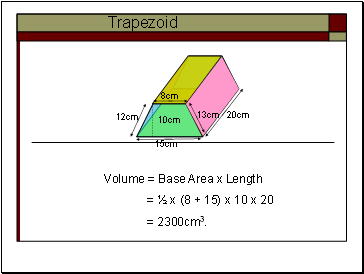
Trapezoid

15cm

8cm

20cm

10cm

Volume = Base Area x Length

= ½ x (8 + 15) x 10 x 20

= 2300cm3.

13cm

12cm

Slide 8

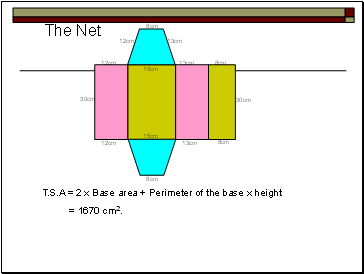
The Net

12cm

13cm

13cm

8cm

8cm

15cm

15cm

30cm

12cm

8cm

8cm

13cm

12cm

30cm

T.S.A = 2 x Base area + Perimeter of the base x height

= 1670 cm2.

Slide 9

THE END

Happiness is not success, But the path leading to success.