Writing linear equations

Page
1

Slide 1

The World Of Linear Equations

Writing Linear Equations

In Slope-Intercept Form

y = mx + b

Slide 2

If you are given: The slope and y-intercept

Finding the equation of the line in y= mx + b form. Given: slope and y-intercept. Just substitute the “m” with the slope value and the “b” with the y-intercept value.

Slope = ½ and

y-intercept = -3

y= mx + b

½

-3

y= ½x – 3

Slide 3

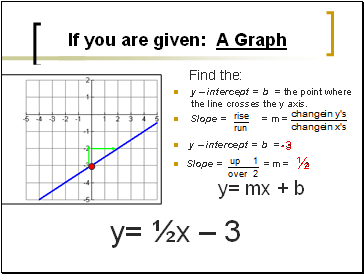
If you are given: A Graph

Find the:

y – intercept = b = the point where the line crosses the y axis.

Slope = = m =

y – intercept = b = -3

Slope = = m = ½

y= mx + b

½

-3

y= ½x – 3

Slide 4

If you are given: The slope and a point

Given: slope (m) and a point (x,y). To write equations given the slope and a point using Point-Slope Form.

Slope =½ and point (4,-1)

½

4

-1

y= ½x – 3

Point-Slope Form

-1 -1

Slide 5

If you are given: The slope and a point

Given: slope (m) and a point (x,y). Substitute x, y, and m into y = mx+b and find the value of b (the y-intercept). Then write the equation substituting m and b values into y = mx + b.

Slope =½ and point (4,-1)

y = mx + b

½

4

-1

y= ½x – 3

-1 = ½(4) + b

-1 = 2 + b

-2 -2

-3 = b So!

m = ½ and b = -3

Slide 6

If you are given: Two points

Finding the equation of the line in y= mx + b form. Given: Two points. First find the slope (m) and then substitute one of the points x and y values into y = mx+b along with the slope.

Point (-2, -4) & Point (2, -2)

Find the:

Slope = = m =

Slope =½ and point (2, -2)

y = mx + b

½

-2

2

-2 = ½(2) + b

y= ½x – 3

-2 = 1 + b

-1 -1

-3 = b So!

m = ½ and b = -3

Slide 7

If you are given: Two points

Finding the equation of the line in y= mx + b form. Given: Two points. First find the slope (m) and then substitute one of the points x and y values into Point-Slope Form.

Point-Slope Form

Point (-2, -4) & Point (2, -2)

Find the:

Slope = = m =

Slope =½ and point (2, -2)

½

-2

2

-2 -2

y= ½x – 3