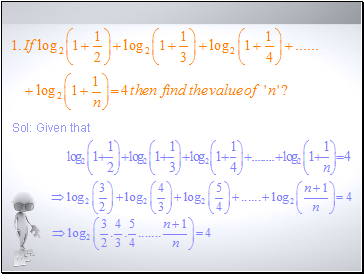Logarithmic Functions

Page
1

Slide 1

Logarithic functions

By

C. SURESH,

Mentor in Mathematics,

APIIIT-Nuzvid,Krishna(Dt.),

A.P., India.

Slide 2

Exponentiation:

The third power of some number ‘b’ is the product of

3 factors of ‘b’. More generally, raising ‘b’ to the n-th power (n is a natural number) is done by multiplying n factors.

Definition:

If b≠1 and ‘y’ are any two positive real numbers then there exists a unique real number ‘x’ satisfying the equation bx = y.

This x is said to be the logarith of y to the base b and is written as

Logb y = x

The idea of logariths is to reverse the operation of exponentiation.

Slide 3

Thus

log3 9 = 2 since 32 = 9

log6 216 = 3 since 63 = 216

log10 0.01 = -2 since 10-2 = 0.01

Similarly

x0 = 1 implies that logx 1 = 0

Note:

Since the exponential function value can never be zero, we can say that logarith of zero is undefined.

2. Similarly, logarithic function is not defined for negative values.

Slide 4

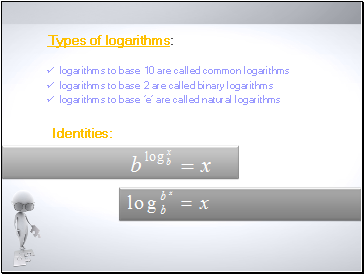
Types of logariths

logariths to base 10 are called common logariths

logariths to base 2 are called binary logariths

logariths to base ‘e’ are called natural logariths

Identities:

Slide 5

Sol: Given that

Slide 6

Slide 7

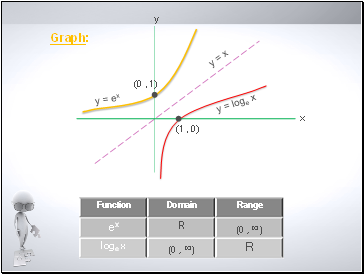
y = loge x

y = ex

Graph:

Slide 8

THANK YOU