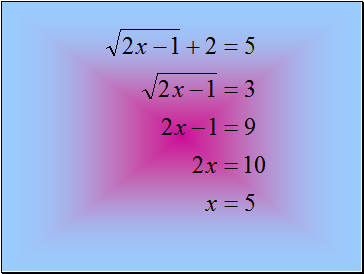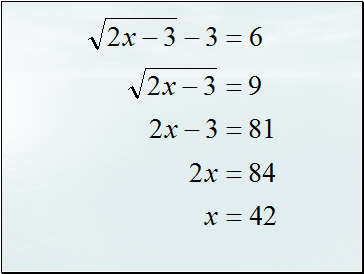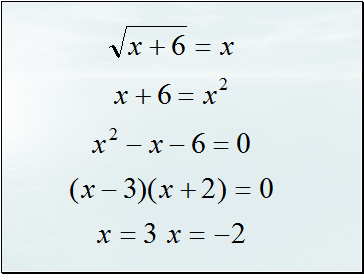Radical Functions and EquationsPage
1
1
Slide 1
Radical
Equations
Slide 2
How Do We Solve Radical Equations?
Do Now: Simplify the given expression.
1. 2.
Slide 3
Radical Equations
An equation in which a variable occurs in the radicand
is called a radical equation. It should be noted, that
when solving a radical equation algebraically,
extraneous roots may be introduced when both sides of
an equation are squared. Therefore, you must check
your solutions for a radical equation.
Solve: √ x - 3 - 3 = 0
√ x - 3 = 3
(√ x - 3 )2 = (3)2
x - 3 = 9
x = 12
Check:
√ x - 3 - 3
√ 12 - 3 - 3
3 - 3
0
0
Therefore, the solution
is x = 12.
x ≥ 3
L.S. R.S.
Slide 4
Slide 5
Slide 6
Slide 7
Slide 8
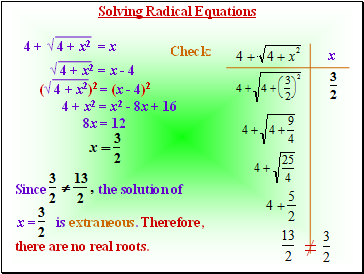
Solving Radical Equations
4 + √ 4 + x2 = x
√ 4 + x2 = x - 4
4 + x2 = x2 - 8x + 16
8x = 12
x
Since
the solution of
x =
is extraneous. Therefore,
there are no real roots.
Check:
≠
(√ 4 + x2)2 = (x - 4)2
Slide 9
Slide 10
Slide 11
Slide 12
x = -1 is an extraneous solution.
Slide 13
Set up the equation so that
there will be one radical on
each side of the equal sign.
Square both sides.
Simplify.
2x + 4 = x + 7
x = 3
Verify your solution.
Therefore, the
solution is
x = 3.
x ≥ -2
Solve
Solving Radical Equations
L.S. R.S.
Slide 14
Squaring a Binomial
(a + 2)2 = a2 + 4a + 4
Note that the middle term is
twice the product of the two
terms of the binomial.
(a√x + b)2
( 5 + √x - 2 )2
The middle term will
Contents
- How Do We Solve Radical Equations?
- Radical Equations
- Solving Radical Equations
- Squaring a Binomial
- One more to see another extraneous solution
- Let's try another one
- Graphing a Radical Function
- Solving a Radical Equation Graphically
- Solving Radical Inequalities
Last added presentations
- The Effects of Radiation on Living Things
- Newton's Laws
- Mechanics Lecture
- Buoyancy
- Practical Applications of Solar Energy
- Newton’s laws of motion
- Sound