Tobacco

Page
1

Slide 1

Tobacco - Inside the Body

Slide 2

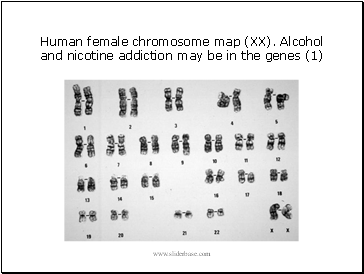
Human female chromosome map (XX). Alcohol and nicotine addiction may be in the genes (1)

Slide 3

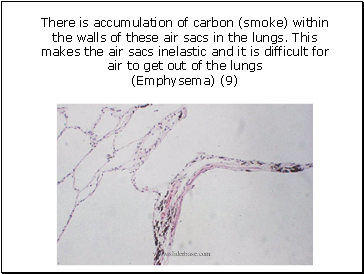
There is accumulation of carbon (smoke) within the walls of these air sacs in the lungs. This makes the air sacs inelastic and it is difficult for air to get out of the lungs (Emphysema) (9)

Slide 4

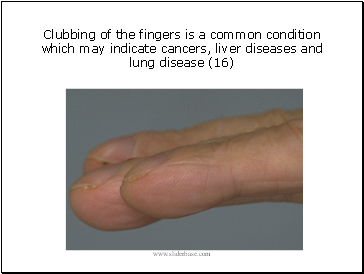
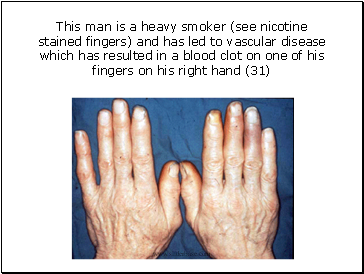
Clubbing of the fingers is a common condition which may indicate cancers, liver diseases and lung disease (16)

Slide 5

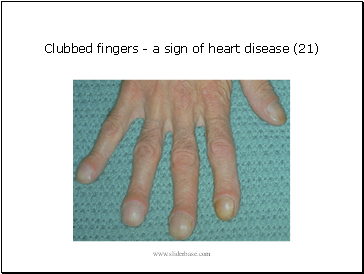
Clubbed fingers

a sign of heart disease (21)

Slide 6

Focal dust emphysema is commonest in cigarette smokers and coal miners.The black colour in this lung is due to cigarette smoke (22)

Slide 7

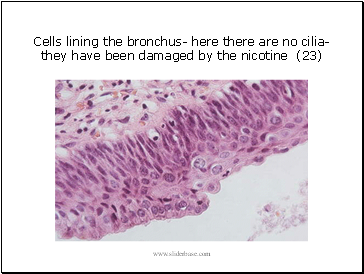
Cells lining the bronchus- here there are no cilia- they have been damaged by the nicotine (23)

Slide 8

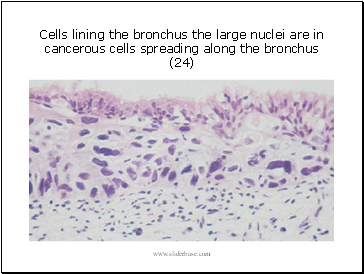
Cells lining the bronchus the large nuclei are in cancerous cells spreading along the bronchus (24)

Slide 9

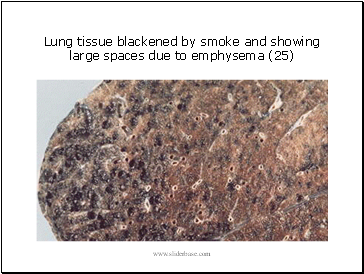
Lung tissue blackened by smoke and showing large spaces due to emphysema (25)

Slide 10

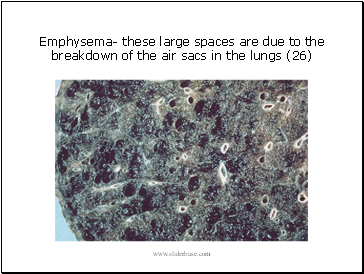
Emphysema

these large spaces are due to the breakdown of the air sacs in the lungs (26)

Slide 11

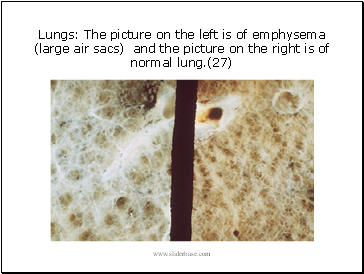
Lungs: The picture on the left is of emphysema (large air sacs) and the picture on the right is of normal lung.(27)

Slide 12

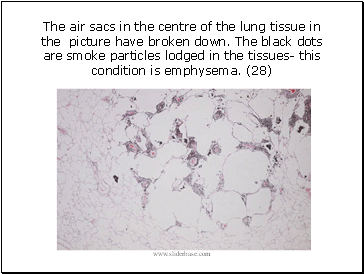
The air sacs in the centre of the lung tissue in the picture have broken down. The black dots are smoke particles lodged in the tissues- this condition is emphysema. (28)

Slide 13

Cancer of the bronchus has spread into the lungs (29)

Slide 14

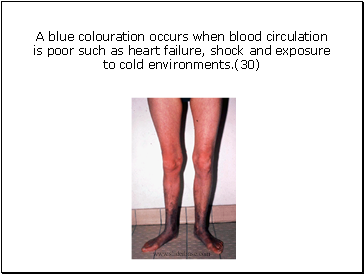
A blue colouration occurs when blood circulation is poor such as heart failure, shock and exposure to cold environments.(30)

Slide 15