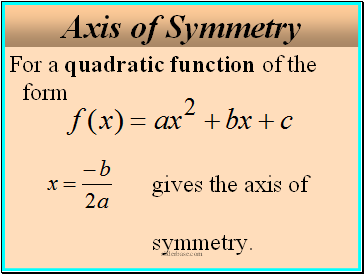Quadratic FunctionsPage
1
1
Slide 1
Quadratic
Functions
Dr. Claude S. Moore Danville Community College
PRECALCULUS I
Slide 2
Polynomial Function
A polynomial function of degree n is where the a’s are real numbers and the n’s are nonnegative integers and an 0.
Slide 3
Quadratic Function
A polynomial function of degree 2 is called a quadratic function.
It is of the form a, b, and c are real numbers and a 0.
Slide 4
Axis of Symmetry
For a quadratic function of the form gives the axis of symmetry.
Slide 5
Standard Form
A quadratic function of the form is in standard form.
axis of symmetry: x = h vertex: (h, k)
Slide 6
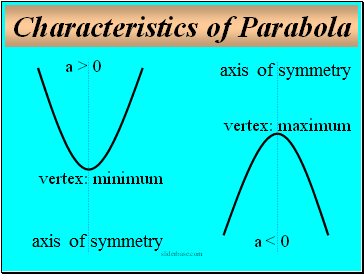
Characteristics of Parabola
a > 0
a < 0
vertex: minimum
vertex: maximum
Slide 7
Higher Degree Polynomial Functions
Dr. Claude S. Moore Danville Community College
PRECALCULUS I
Slide 8
Characteristics
The graph of a polynomial function…
1. Is continuous.
2. Has smooth, rounded turns.
3. For n even, both sides go same way.
4. For n odd, sides go opposite way.
5. For a > 0, right side goes up.
6. For a < 0, right side goes down.
Slide 9
.
an < 0
graphs of a polynomial function for n odd:
Leading Coefficient Test: n odd
an > 0
Slide 10
.
an < 0
graphs of a polynomial function for n even:
an > 0
Leading Coefficient Test: n even
Slide 11
Roots, Zeros, Solutions
The following statements are equivalent for
real number a and polynomial function f :
1. x = a is root or zero of f.
2. x = a is solution of f (x) = 0.
3. (x - a) is factor of f (x).
4. (a, 0) is x-intercept of graph of f (x).
Slide 12
1. If a polynomial function contains a factor (x - a)k, then x = a is a repeated root of multiplicity k.
2. If k is even, the graph touches (not crosses) the x-axis at x = a.
Contents
- Polynomial Function
- Quadratic Function
- Axis of Symmetry
- Standard Form
- Characteristics of Parabola
- Characteristics
- Roots, Zeros, Solutions
- Intermediate Value Theorem
- NOTE to Intermediate Value
- Full Division Algorith
- Short Division Algorith
- Synthetic Division
- Remainder Theorem
- Factor Theorem
- Descartes’s Rule of Signs
- Rational Zero Test
- Upper and Lower Bound
Last added presentations
- Mechanical, Electromagnetic, Electrical, Chemical and Thermal
- Mechanics Lecture
- The Effects of Radiation on Living Things
- Soil and Plant Nutrition
- Newton’s law of universal gravitation
- Radioactivity and Nuclear Reactions
- Sound