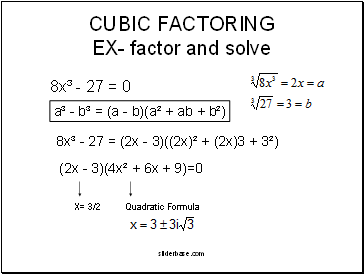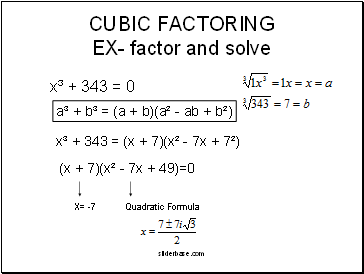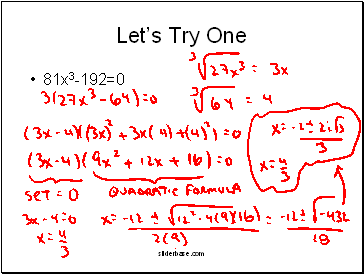Solving Polynomial Equations

Page
1

Slide 1

Solving Polynomial Equations

Slide 2

One of the topics in this section is finding the cube or cube root of a number.

A cubed number is the solution when a number is multiplied by itself three times.

A cube root “undos” the cubing operation just like a square root would.

Slide 3

Calculator Function – How to take the cube root of a number

To take the cube root of a number, press MATH, then select option 4.

Example: What is ?

24

Slide 4

Solving Polynomials by Graphing

We start getting into more interesting equations now . . .

Ex: x3 + 3x2 = x + 3

Problem: Solve the equation above, using a graphing calculator

Slide 5

Solving Polynomials by Graphing

What about something like this???

Ex: x3 + 3x2 + x = 10

Use the same principal; plug the first part of the equation in for Y1; the solution (10) for Y2; then find the intersection of the two graphs.

Slide 6

Factoring and roots cubic factoring

a³ + b³ = (a + b)(a² - ab + b²)

a³ - b³ = (a - b)(a² + ab + b²)

Difference of Cubes

Sum of Cubes

Question: if we are solving for x, how many possible answers can we expect?

3 because it is a cubic!

Slide 7

CUBIC FACTORING EX- factor and solve

8x³ - 27 = 0

8x³ - 27 = (2x - 3)((2x)² + (2x)3 + 3²)

(2x - 3)(4x² + 6x + 9)=0

Quadratic Formula

X= 3/2

a³ - b³ = (a - b)(a² + ab + b²)

Slide 8

CUBIC FACTORING EX- factor and solve

x³ + 343 = 0

a³ + b³ = (a + b)(a² - ab + b²)

x³ + 343 = (x + 7)(x² - 7x + 7²)

(x + 7)(x² - 7x + 49)=0

Quadratic Formula

X= -7

Slide 9

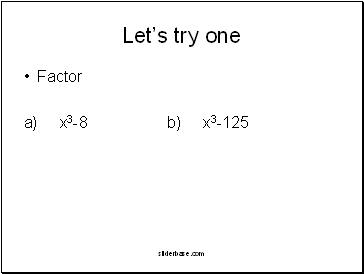
Let’s try one

Factor

a) x3-8 b) x3-125

Slide 10

Let’s try one

Factor

a) x3-8 b) x3-125

Slide 11

Let’s Try One

81x3-192=0

Hint: IS there a GCF???

Slide 12