Ten Ways of Looking at Real Numbers

Page
1

Slide 1

Ten Ways of Looking at Real Numbers

Robert Mayans

Department of Math/CSci/Physics

Fairleigh Dickinson University

Slide 2

Varieties of Mathematical Text

Books

Reference books

Text books

Lecture Notes

Handbooks and encyclopedias

Slide 3

Varieties of Mathematical Text

Papers

Research papers

Survey articles

Collected works

Online Resources

MathSciNet

Online databases

E-journals

Slide 4

The Mathematics Hypertext Project (MHP)

A Web-based hypertext of mathematics

A design paper describes goals, organization, technology issues, etc.

http://jodi.ecs.soton.ac.uk/Articles/v05/i01/Mayans/jodi/

First release in June, 2005

This presentation discusses some of the pages on the real numbers

Slide 5

Slide 6

Text on Real Numbers

We aim for a “comprehensive introduction" to the real numbers.

Real numbers are everywhere dense in mathematics.

Real numbers have different meanings in different contexts.

Slide 7

Text on Real Numbers

What to include on a text on real numbers?

Foundations and construction of real numbers

Characterizations of the real numbers by structure.

Extensions and substructures of the real numbers

Real numbers classified in different ways.

Real numbers are a system related to other systems.

Slide 8

#1. Foundations of the Real Number System

How to define real numbers and their basic operations from rationals or integers

Presentation of three methods

Dedekind cuts of rational numbers

Equivalence classes of Cauchy sequences of rational numbers

Base-10 digit sequences

Slide 9

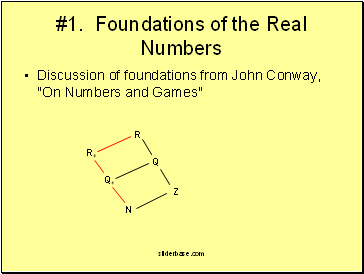
#1. Foundations of the Real Numbers

Discussion of foundations from John Conway, "On Numbers and Games"

N

Z

Q+

Q

R+

R

Slide 10

#2. Real Numbers as a Linear Order

The real numbers form the unique linear order that is:

dense

without endpoints

Dedekind-complete

separable (countable dense subset)

Slide 11