Optical Illusions

Page
2

A' x' = b' + ε.

We are dealing with what is called the errors-in-variable model in statistics. We have to use an estimator, that is a procedure, to solve the equation system. The most common choice is by means of least squares (LS) estimation. However, it is well known, that LS estimation is biased.

Under some simplifying assumptions (identical and independent random variables δA and δb with zero mean and variance σ2 ) the LS estimate converges to

Large variance in δA , an ill-conditioned A', or an x' which is oriented close to the eigenvector of the smallest singular value of A' all could increase the bias and push the LS solution away from the real solution. Generally it leads to an underestimation of the parameters.

There are other, more elaborate estimators that could be used. None, however will perform better if the errors cannot be obtained with high accuracy.

Examples of visual computations which amount to linear equation systems are the estimation of image motion or optical flow, the estimation of the intersections of lines, and the estimation of shape from various cues, such as motion, stereo, texture, or patterns.

Slide 4

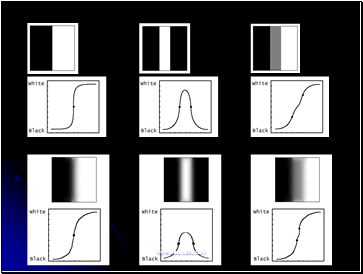
Errors in Image Intensity: How images change when smoothed

As a noisy version of the ideal image signal

We create the most likely image the vision system works with by smoothing the image

Many illusions can be understood from the behavior of straight lines and edges

Three cases

An edge at the border between regions of different intensity, such as black and white

No change

A line on a background of different intensity

Drift apart each other

A gray line between a bright and a dark region

Move toward each other

Slide 5

Slide 6

Errors in Image Intensity: Café Wall Illusion

The horizontal mortar lines being tilted

Effects of smoothing

Slide 7

Errors in Image Intensity: Café Wall Illusion

Local edge detection  linked to longer lines

Slide 8

Errors in Image Intensity: Café Wall Illusion

Counteract the effect

Slide 9

Errors in Image Intensity: Spring Pattern

Square grid with black squares superimposed

Slide 10

Errors in Image Intensity: Spring Pattern

Combination of type-1 (single) and type-2 (drift apart) edges