Optical Illusions

Page
3

Flash Anim

Slide 11

Errors in Image Intensity: Waves Pattern

Black and white checkerboard with small squares

Flash Anim

Slide 12

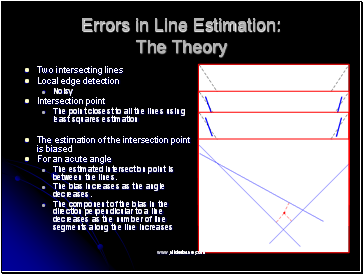
Errors in Line Estimation: The Theory

Two intersecting lines

Local edge detection

Noisy

Intersection point

The point closest to all the lines using least squares estimation

The estimation of the intersection point is biased

For an acute angle

The estimated intersection point is between the lines.

The bias increases as the angle decreases.

The component of the bias in the direction perpendicular to a line decreases as the number of line segments along the line increases

Slide 13

The two ends of the straight diagonal line passing behind the rectangle appear to be offset

Can be predicted by the bias

The diagonal line segments

The lines at the border of the rectangle

The illusory effect increases with a decrease in the acute angle

Errors in Line Estimation: Poggendorff Illusion

Java Anim

Slide 14

Errors in Line Estimation: Zöllner Illusion

Tilted segments are estimated

Input to the higher computational processes which fits long line to the segments

Parametric studies

A stronger illusory perception for more tilted obliques

A stronger illusory effect when the pattern is rotated by 45 degrees

In neurophysiological studies, our cortex responds more to lines in horizontal and vertical than oblique orientations

Less response from the main lines, more bias

Java Anim

Slide 15

Errors in Line Estimation: Luckiesh Pattern

Distorted circle

The bias depends on the direction of the intersecting lines

Changing the direction of the background lines causes a change in the bias and thus a change in the estimated curve, with the circle bumping at different locations

Java Anim

Slide 16

Errors in Movement: How image movement is estimated

Optical flow

Representation of image motion by comparing sequential images and estimating how patterns move between images

The movement of the point from the first image to the second image. It can only be computed where there is detail, or edges, in the image. And it requires two computational stages to estimate optical flow.

Normal flow (First stage)

Through a small aperture, we can only compute the component of the motion vector perpendicular the edge

Local information only provides information about the line