Acoustics of Concert Halls and Rooms

Page
1

Slide 1

Acoustics of Concert Halls and Rooms

SOUND WAVES AND SOUND FIELDS

Principles of Sound and Vibration, Chapter 6

Science of Sound, Chapter 6

Slide 2

The acoustic wave equation

The acoustic wave equation is generally derived by

considering an ideal fluid (a mathematical fiction).

Its motion is described by the Euler equation of motion.

In a real fluid (with viscosity), the Euler equation is

Replaced by the Navier-Stokes equation.

Two different notations are used to derive the Acoustic wave

equation:

The LaGrange description

We follow a “particle” of fluid as it is compressed as well as displaced by an acoustic wave.)

The Euler description

(Fixed coordinates; p and c are functions of x and t.

They describe different portions of the fluid as it streams past.

Slide 3

PLANE SOUND WAVES

Slide 4

Plane Sound Waves

Slide 5

SPHERICAL WAVES

We can simplify matters even further by writing p = ψ/r, giving

(a one dimensional wave equation)

Slide 6

Spherical waves:

Particle (acoustic) velocity:

Impedance:

The solution is an outgoing plus an incoming wave

ρc at kr >> 1

Similar to:

ρ ∂2ξ/∂t2 = -∂p/∂x

outgoing incoming

Slide 7

SOUND PRESSURE, POWER AND LOUDNESS

Decibels

Decibel difference between two power levels:

ΔL = L2 – L1 = 10 log W2/W1

Sound Power Level: Lw = 10 log W/W0 W0 = 10-12 W

(or PWL)

Sound Intensity Level: LI = 10 log I/I0 I0 = 10-12 W/m2

(or SIL)

Slide 8

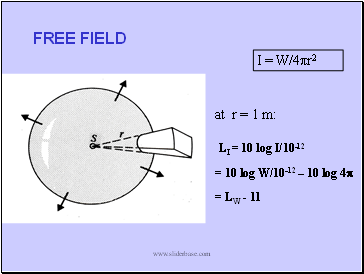
FREE FIELD

I = W/4πr2

at r = 1 m:

LI = 10 log I/10-12

= 10 log W/10-12 – 10 log 4p

= LW - 11

Slide 9

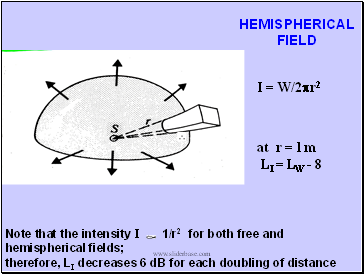
HEMISPHERICAL FIELD

I = W/2pr2

at r = l m

LI = LW - 8

Note that the intensity I 1/r2 for both free and hemispherical fields;

therefore, LI decreases 6 dB for each doubling of distance

Slide 10

Sound pressure level

Our ears respond to extremely small pressure

fluctuations p

Intensity of a sound wave is proportional to the sound