Gravitation

Page
2

Slide 10

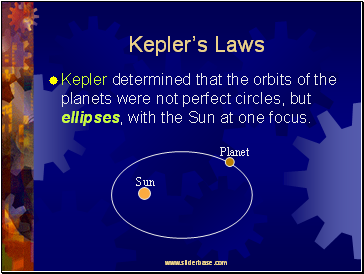
Kepler’s Laws

Kepler determined that the orbits of the planets were not perfect circles, but ellipses, with the Sun at one focus.

Slide 11

Kepler’s Second Law

Kepler determined that a planet moves faster when near the Sun, and slower when far from the Sun.

Faster

Slower

Slide 12

Why?

Kepler’s Laws provided a complete kinematical description of planetary motion (including the motion of planetary satellites, like the Moon) - but why did the planets move like that?

Slide 13

The Apple & the Moon

Isaac Newton realized that the motion of a falling apple and the motion of the Moon were both actually the same motion, caused by the same force - the gravitational force.

Slide 14

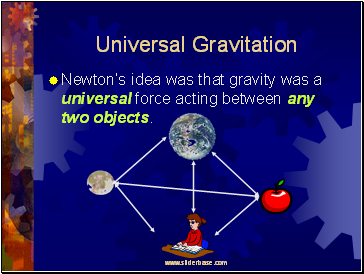
Universal Gravitation

Newton’s idea was that gravity was a universal force acting between any two objects.

Slide 15

At the Earth’s Surface

Newton knew that the gravitational force on the apple equals the apple’s weight, mg, where g = 9.8 m/s2.

W = mg

Slide 16

Weight of the Moon

Newton reasoned that the centripetal force on the moon was also supplied by the Earth’s gravitational force.

Fc = mg

?

Slide 17

Weight of the Moon

Newton’s calculations showed that the centripetal force needed for the Moon’s motion was about 1/3600th of Mg, however, where M is the mass of the Moon.

Slide 18

Weight of the Moon

Newton knew, though, that the Moon was about 60 times farther from the center of the Earth than the apple.

And 602 = 3600

Slide 19

Universal Gravitation

From this, Newton reasoned that the strength of the gravitational force is not constant, in fact, the magnitude of the force is inversely proportional to the square of the distance between the objects.

Slide 20

Universal Gravitation

Newton concluded that the gravitational force is:

Directly proportional to the masses of both objects.

Inversely proportional to the distance between the objects.