Sound

Page
8

Slide 30

Acoustics

Acoustics sometimes refers to the science of sound. It can also refer to how well sounds traveling in enclosed spaces can be heard. The Great Hall in the Krannert Center is an example of excellent acoustics. Chicago Symphony Orchestra has even recorded there. Note how the walls and ceiling are beveled to get sound waves reflect in different directions. This minimizes the odds of there being a “dead spot” somewhere in the audience.

Click and scroll down to zoom in on the Great Hall pic.

Slide 31

Standing Waves: 2 Fixed Ends

When a guitar string of length L is plucked, only certain frequencies can be produced, because only certain wavelengths can sustain themselves. Only standing waves persist. Many harmonics can exist at the same time, but the fundamental (n = 1) usually dominates. As we saw in the wave presentation, a standing wave occurs when a wave reflects off a boundary and interferes with itself in such a way as to produce nodes and antinodes. Destructive interference always occurs at a node. Both types occur at an antinode; they alternate.

Animation: Harmonics 1, 2, & 3

n = 1 (fundamental)

Node Antinode

n = 2

Slide 32

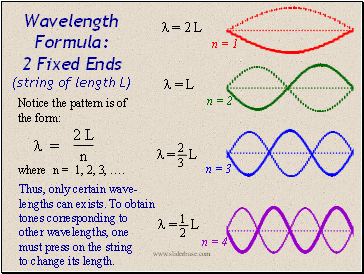
Wavelength Formula: 2 Fixed Ends (string of length L)

n = 1

n = 2

n = 3

 = 2 L

 = L

 = L

2 3

n = 4

 = L

1 2

Notice the pattern is of the form:

Thus, only certain wave-lengths can exists. To obtain tones corresponding to other wavelengths, one must press on the string to change its length.

where n = 1, 2, 3, ….

Slide 33

Vibrating String Example

Schmedrick decides to build his own ukulele. One of the four strings has a mass of 20 g and a length of 38 cm. By turning the little knobby, Schmed cranks up the tension in this string to 300 N. What frequencies will this string produced when plucked? Hints:

1. Calculate the string’s mass per unit length, :

2. How the speed of a wave traveling on this string using the formula v = F /  from last chapter:

3. Calculate several wavelengths of standing waves on this string:

4. Calculate the corresponding frequencies:

Hear what a ukulele sounds like. (Scroll down.)

75.498 m / s

0.0526 kg / m

0.76 m, 0.38 m, 0.2533 m

99 Hz, 199 Hz, 298 Hz

Slide 34

Standings Waves in a Tube: 2 Open Ends

Like waves traveling on a string, sound waves traveling in a tube reflect back when they reach the end of the tube. (Much of the sound energy will exit the open tube, but some will reflect back.) If the wavelength is right, the reflected waves will combine with the original to create a standing wave. For a tube with two open ends, there will be an antinode at each end, rather than a node. (A closed end would correspond to a node, since it blocks the air from moving.) The pic shows the fundamental. Note: the air does not move like a guitar string moves; the curve represents the amount of vibration. Maximum vibration occurs at the antinodes. In the middle is a node where the air molecules don’t vibrate at all.