Cartesian components

Page
1

Slide 1

CARTESIAN COMPONENTS OF VECTORS

Slide 2

Two-dimensional Coordinate frames

The diagram shows a two-dimensional coordinate frame.

Any point P in the plane of the figure can be defined in terms of its x and y coordinates.

Slide 3

A unit vector pointing in the positive direction of the x-axis is denoted by i.

Any vector in the direction of the x-axis will be a multiple of i.

A vector of length l in the direction of the x-axis can be written li.

(All these vectors are multiples of i.)

Slide 4

(All these vectors are

multiples of j.)

A unit vector pointing in the positive direction of the y-axis is denoted by j.

Any vector in the direction of the y-axis will be a multiple of j.

A vector of length l in the direction of the y-axis can be written lj.

Slide 5

Key Point

i represents a unit vector in the direction of the positive x-axis.

j represents a unit vector in the direction of the positive y-axis.

Slide 6

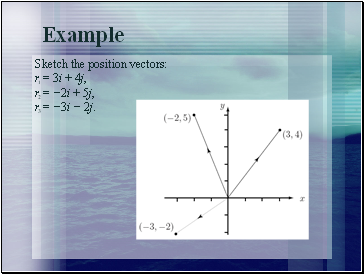
Example

Draw the vectors 5i and 4j. Use your diagram and the triangle law of addition to add these two vectors together.

Slide 7

Any vector in the xy plane can be expressed in the form

r = ai + bj

The numbers a and b are called the components of r in the

x and y directions.

Slide 8

a) Draw an xy plane and show the vectors p = 2i + 3j, and q = 5i + j.

b) Express p and q using column vector notation.

c) Show the sum p + q.

d) Express the resultant p + q in terms of i and j.

Example

Slide 9

If a = 9i + 7j and b = 8i + 3j, find:

a) a + b

b) a − b

Example

Slide 10

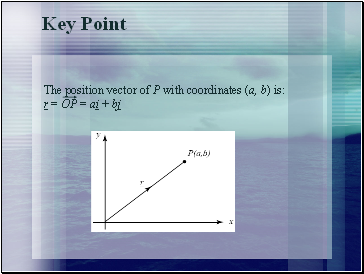
Key Point

The position vector of P with coordinates (a, b) is:

r = OP = ai + bj

Slide 11

State the position vectors of the points with coordinates:

a) P(2, 4)

b) Q(−1, 5)

c) R(−1,−7)

d) S(8,−4)

Example

Slide 12