Geometry of shapes

Page
2

If a parallelogram has an area of A square units, a base of b units and a height of h units, then A = bh. (Do example 1 p. 530)

The area of a region is the sum of the areas of all its non-overlapping parts. (Do example 3 p. 531)

b

h

Slide 9

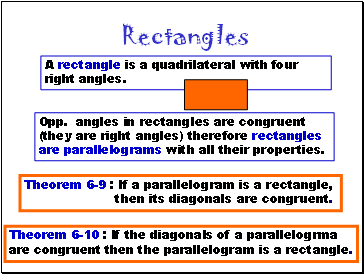
Rectangles

A rectangle is a quadrilateral with four right angles.

Theorem 6-9 : If a parallelogram is a rectangle,

then its diagonals are congruent.

Opp. angles in rectangles are congruent (they are right angles) therefore rectangles are parallelograms with all their properties.

Theorem 6-10 : If the diagonals of a parallelogrma

are congruent then the parallelogram is a rectangle.

Slide 10

Rectangles (2)

If a quadrilateral is a rectangle, then the following properties hold true:

Opp. Sides are congruent and parallel

Opp. Angles are congruent

Consecutive angles are supplementary

Diagonals are congruent and bisect each other

All four angles are right angles

Slide 11

Squares and Rhombi

A rhombus is a quadrilateral with four congruent sides. Since opp. sides are  , a rhombus is a parallelogram with all its properties.

Special facts about rhombi

Theorem 6.11: The diagonals of a rhombus

are perpendicular.

Theorem 6.12: If the diagonals of a parallelogram are perpendicular, then the parallelogram is a rhombus.

Theorem 6.13: Each diagonal of a rhombus bisects

a pair of opp. angles

C

Slide 12

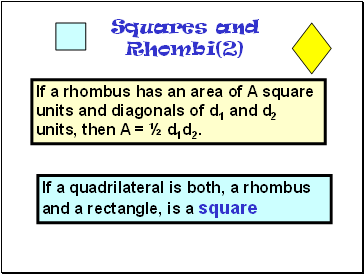
Squares and Rhombi(2)

If a quadrilateral is both, a rhombus and a rectangle, is a square

If a rhombus has an area of A square units and diagonals of d1 and d2 units, then A = ½ d1d2.

Slide 13

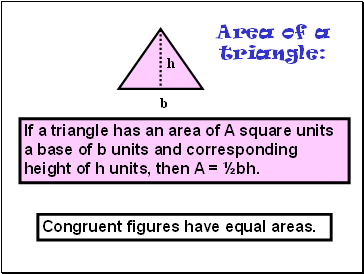
Area of a triangle

If a triangle has an area of A square units a base of b units and corresponding height of h units, then A = ½bh.

h

b

Congruent figures have equal areas.

Slide 14

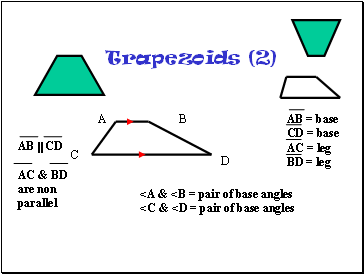
Trapezoids

A trapezoid is a quadrilateral with exactly one pair of parallel sides.

The parallel sides are called bases.

The nonparallel sides are called legs.

At each side of a base there is a pair of base angles.

C

Slide 15

Trapezoids (2)

C

A

C

D

B

AB = base

CD = base

AC = leg

BD = leg

AB  CD

AC & BD are non parallel

<A & <B = pair of base angles