Geometry of shapes

Page
1

Slide 1

Parallelograms

Quadrilaterals are four-sided polygons

Parallelogram: is a quadrilateral with both pairs of opposite sides parallel.

Slide 2

Parallelograms (2)

Theorem 6.1 : Opposite sides of a parallelograms are congruent

Theorem 6.2: Opposite angles of a parallelogram are congruent

Theorem 6.3: Consecutive angles in a parallelogram

are supplementary.

A

D

C

B

AD  BC and AB  DC

<A  <C and <B  <D

m<A+m<B = 180°

m <B+m<C = 180°

m<C+m<D = 180°

m<D+m<A = 180°

Slide 3

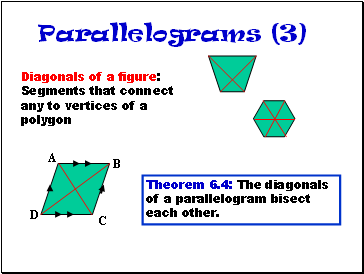
Parallelograms (3)

Diagonals of a figure: Segments that connect any to vertices of a polygon

Theorem 6.4: The diagonals of a parallelogram bisect each other.

A

B

C

D

Slide 4

Parallelograms (4)

Draw a parallelogram : ABCD on a piece of construction paper.

Cut the parallelogram.

Fold the paper and make a crease from A to C and from B to D.

Fold the paper so A lies on C. What do you observe?

Fold the paper so B lies on D. What do you observe?

What theorem is confirmed by these Observations?

Slide 5

Tests for Parallelograms

Theorem 6.5 :If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

Theorem 6.6: If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

A

D

C

B

If AD  BC and AB  DC, then ABCD is a parallelogram

If <A  <C and <B  <D, then ABCD is a parallelogram

Slide 6

Tests for Parallelograms 2

Theorem 6.7: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram

A

D

C

B

Theorem 6.8: If one pair of opposite sides of a quadrilateral is both parallel and congruent, then the quadrilateral is a parallelogram.

Slide 7

A quadrilateral is a parallelogram if .

Diagonals bisect each other. (Theorem 6.7)

A pair of opposite sides is both parallel and congruent. (Theorem 6.8)

Both pairs of opposite sides are congruent. (Theorem 6.5)

Both pairs of opposite angles are congruent. (Theorem 6.6)

Both pairs of opposite sides are parallel. (Definition)

Slide 8

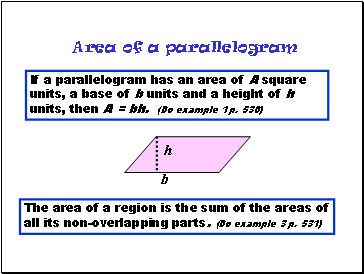
Area of a parallelogram