Chemical Equilibrium

Page
2

For the gas phase reaction:

3H2(g) + N2(g)  2NH3(g)

Slide 12

Heterogeneous Equilibria

The position of a heterogeneous equilibrium does not depend on the amounts of pure solids or liquids present

Write the equilibrium expression for the reaction:

PCl5(s)  PCl3(l) + Cl2(g)

Pure

solid

Pure

liquid

Slide 13

The Reaction Quotient

For some time, t, when the system is not at equilibrium, the reaction quotient, Q takes the place of K, the equilibrium constant, in the law of mass action.

jA + kB  lC + mD

Slide 14

Significance of the Reaction Quotient

If Q = K, the system is at equilibrium

If Q > K, the system shifts to the left, consuming products and forming reactants until equilibrium is achieved

If Q < K, the system shifts to the right, consuming reactants and forming products until equilibrium is achieved

Slide 15

Solving for Equilibrium Concentration

Consider this reaction at some temperature:

H2O(g) + CO(g)  H2(g) + CO2(g) K = 2.0

Assume you start with 8 molecules of H2O and 6 molecules of CO. How many molecules of H2O, CO, H2, and CO2 are present at equilibrium?

Here, we learn about “ICE” – the most important problem solving technique in the second semester. You will use it for the next 4 chapters!

Slide 16

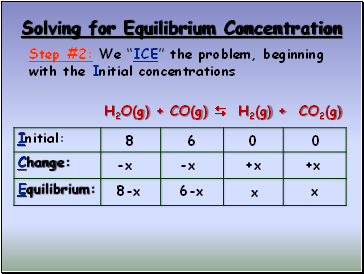
Solving for Equilibrium Concentration

H2O(g) + CO(g)  H2(g) + CO2(g) K = 2.0

Step #1: We write the law of mass action for the reaction:

Slide 17

Solving for Equilibrium Concentration

H2O(g) + CO(g)  H2(g) + CO2(g)

Step #2: We “ICE” the problem, beginning with the Initial concentrations

8

6

0

0

-x

-x

+x

+x

8-x

6-x

x

x

Slide 18

Solving for Equilibrium Concentration

Step #3: We plug equilibrium concentrations into our equilibrium expression, and solve for x

H2O(g) + CO(g)  H2(g) + CO2(g)

x = 4

Slide 19

Solving for Equilibrium Concentration

Step #4: Substitute x into our equilibrium concentrations to find the actual concentrations

H2O(g) + CO(g)  H2(g) + CO2(g)

x = 4