Gravity and Circular Motion Revision

Page
1

Slide 1

Gravity and Circular Motion Revision AQA syllabus A Section 13.3.1-6

B.W.Hughes

Slide 2

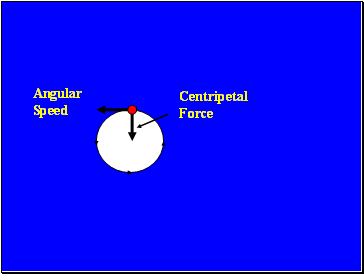
Circular motion

When an object undergoes circular motion it must experience a

centripetal force

This produces an acceleration

towards the centre of the circle

Slide 3

Angular Speed

Centripetal Force

Slide 4

Slide 5

Slide 6

Slide 7

Angular speed

Angular speed can be measured in ms-1 or

Rads-1 (radians per second) or

Revs-1 (revolutions per second)

The symbol for angular speed in radians per second is

ω

Slide 8

Converting to ω

To convert v to ω

ω = v/r

To convert revs per second to ω

Multiply by 2π

Slide 9

Acceleration

The acceleration towards the centre of the circle is

a = v2/r OR

a = ω2r

Slide 10

Centripetal Force Equation

The general force equation is

F = ma

so the centripetal force equation is

F = mv2/r OR

F = m ω2r

THESE EQUATIONS MUST BE LEARNED!!

Slide 11

Example

Gravity provides the accelerating force to keep objects in contact with a humpback bridge. What is the minimum radius of a bridge that a wheel will stay in contact with the road at 10 ms-1?

v = 10 ms-1, g = 10 ms-2, r = ?

a = v2/r = g so r = v2/g

r = 102/10 = 10 m

Slide 12

Newton’s Gravitation Equation

Newton’s Gravitation equation is

F = -Gm1m2/r2

MUST BE LEARNED!!

Negative sign is

a vector sign

G is

Universal Gravitational Constant

Slide 13

More about the equation

m1 and m2 are

the two gravitating masses

r is

the distance between their centres of gravity

The equation is an example of an

Inverse square law

Slide 14