Dividing Polynomials

Page
1

Slide 1

Dividing Polynomials

Slide 2

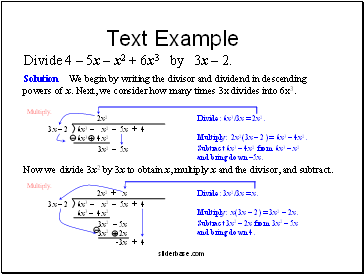
Long Division of Polynomials

Arrange the terms of both the dividend and the divisor in descending powers of any variable.

Divide the first term in the dividend by the first term in the divisor. The result is the first term of the quotient.

Multiply every term in the divisor by the first term in the quotient. Write the resulting product beneath the dividend with like terms lined up.

Subtract the product from the dividend.

Bring down the next term in the original dividend and write it next to the remainder to form a new dividend.

Use this new expression as the dividend and repeat this process until the remainder can no longer be divided. This will occur when the degree of the remainder (the highest exponent on a variable in the remainder) is less than the degree of the divisor.

Slide 3

Text Example

Divide 4 – 5x – x2 + 6x3 by 3x – 2.

Slide 4

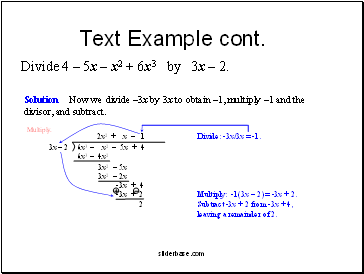
Text Example cont.

Divide 4 – 5x – x2 + 6x3 by 3x – 2.

Slide 5

The Division Algorith

If f (x) and d(x) are polynomials, with d(x) = 0, and the degree of d(x) is less than or equal to the degree of f (x), then there exist unique polynomials q(x) and r(x) such that

f (x) = d(x) • q(x) + r(x).

The remainder, r(x), equals 0 or its is of degree less than the degree of d(x). If r(x) = 0, we say that d(x) divides evenly in to f (x) and that d(x) and q(x) are factors of f (x).

Slide 6

Synthetic Division

To divide a polynomial by x – c

Example

1. Arrange polynomials in descending powers,

with a 0 coefficient for any missing terms. x – 3 x3 + 4x2 – 5x + 5

2. Write c for the divisor, x – c. To the right, 3 1 4 -5 5

write the coefficients of the dividend.

3. Write the leading coefficient of the dividend 3 1 4 -5 5

on the bottom row. Bring down 1.

1

4. Multiply c (in this case, 3) times the value 3 1 4 -5 5

just written on the bottom row. Write the 3

product in the next column in the 2nd row. 1

Slide 7

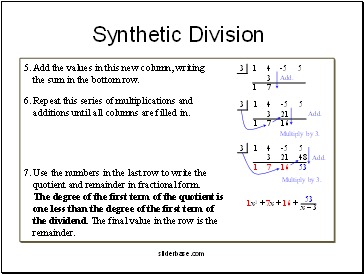
5. Add the values in this new column, writing

the sum in the bottom row.

6. Repeat this series of multiplications and

additions until all columns are filled in.

7. Use the numbers in the last row to write the

quotient and remainder in fractional form.

The degree of the first term of the quotient is