Properties of Functions

Page
1

Slide 1

Properties of Functions

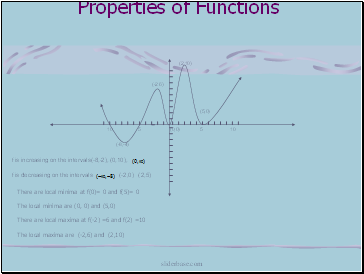
There are local minima at f(0)= 0 and f(5)= 0

The local minima are (0, 0) and (5,0)

There are local maxima at f(-2) =6 and f(2) =10

The local maxima are (-2,6) and (2,10)

(-8,-4)

(-2 6)

(2,10)

(5,0)

f is increasing on the intervals(-8,-2), (0,10),

f is decreasing on the intervals (-2,0) (2,5)

sliderbase.com

Slide 2

Library of Functions

Linear Function

The graph of a linear function is a non-vertical line. A linear function is of the form

y = f(x) = mx + b where m and b are real numbers.

Here m is the slope and b is the y - intercept.

To find the x - intercept let y = 0 and solve for x

The domain and range of a linear function are all real numbers.

Graph

sliderbase.com

Slide 3

Example

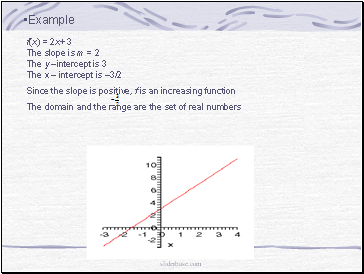
f(x) = 2x+ 3

The slope is m = 2

The y –intercept is 3

The x – intercept is –3/2

Since the slope is positive, f is an increasing function

The domain and the range are the set of real numbers

sliderbase.com

Slide 4

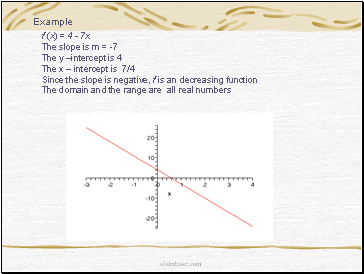
f (x) = 4 - 7x

The slope is m = -7

The y –intercept is 4

The x – intercept is 7/4

Since the slope is negative, f is an decreasing function

The domain and the range are all real numbers

Example

sliderbase.com

Slide 5

The constant function

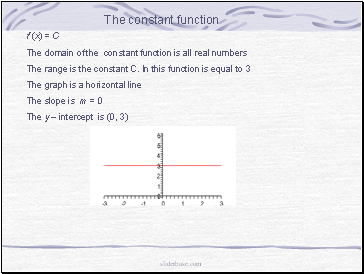
f (x) = C

The domain of the constant function is all real numbers

The range is the constant C. In this function is equal to 3

The graph is a horizontal line

The slope is m = 0

The y – intercept is (0, 3)

sliderbase.com

Slide 6

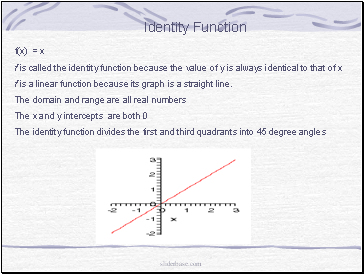
Identity Function

f(x) = x

f is called the identity function because the value of y is always identical to that of x

f is a linear function because its graph is a straight line.

The domain and range are all real numbers

The x and y intercepts are both 0

The identity function divides the first and third quadrants into 45 degree angles

sliderbase.com

Slide 7

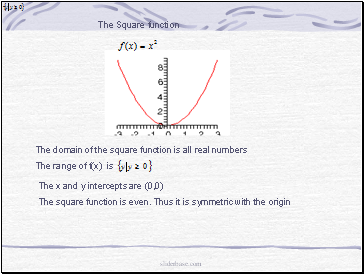
The Square function

The domain of the square function is all real numbers

The range of f(x) is

The x and y intercepts are (0,0)

The square function is even. Thus it is symmetric with the origin

sliderbase.com

Slide 8

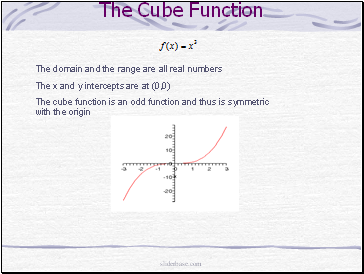
The Cube Function