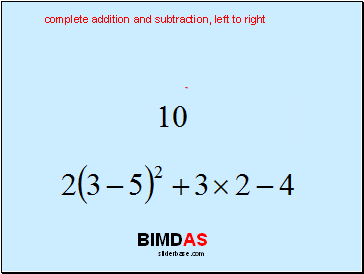Real Numbers

Page
1

Slide 1

Real numbers

Slide 2

{1, 2, 3, 4, . . . }

If you were asked to count, the numbers you’d say are called counting numbers. These numbers can be expressed using set notation.

These are also called the natural numbers.

{0, 1, 2, 3, 4, . . . }

If we include 0 we have the set of whole numbers.

{ …, -3, -2, -1, 0,1, 2, 3, . . . }

Include the opposites of the whole numbers and you have the set of integers.

Slide 3

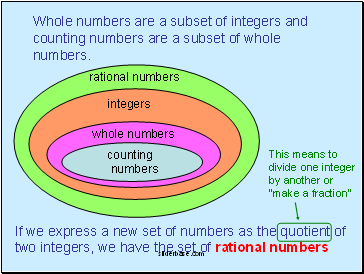
Whole numbers are a subset of integers and counting numbers are a subset of whole numbers.

If we express a new set of numbers as the quotient of two integers, we have the set of rational numbers

This means to divide one integer by another or “make a fraction”

Slide 4

rational numbers

There are numbers that cannot be expressed as the quotient of two integers. These are called irrational numbers.

irrational

numbers

The rational numbers combined with the irrational numbers make up the set of real numbers.

REAL NUMBERS

Slide 5

Translating English to Maths

=

ab

a - b

a + b

Slide 6

Order of operations

When there is more than one symbol of operation in an expression, it is agreed to complete the operations in a certain order. A mnemonic to help you remember this order is below.

B I M D A S

rackets

ndices

ultiplication

ivision

ddition

ubtraction

Do any simplifying possible inside of brackets starting with innermost brackets and working out

Apply Indices

Complete multiplication and division from left to right

Complete addition and subtraction from left to right

Slide 7

BIMDAS

BIMDAS

brackets – combine these first

BIMDAS

indices – apply the indice now

BIMDAS

complete multiplication and division, left to right

BIMDAS

complete addition and subtraction, left to right

Slide 8

Commutative property

The operations of both addition and multiplication are commutative

When adding, you can “commute” or trade the terms places

When multiplying, you can “commute” or trade the factors places

Slide 9

Associative property