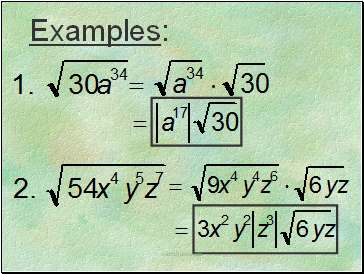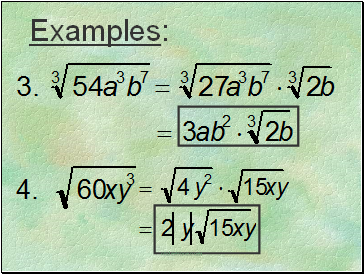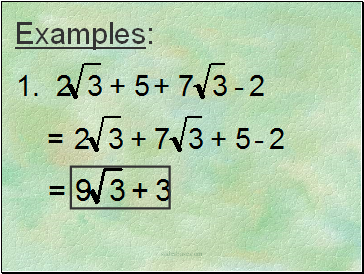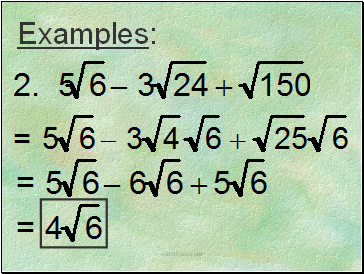Simplifying Radical Expressions

Page
1

Slide 1

Simplifying Radical Expressions

Slide 2

Product Property of Radicals

Slide 3

Product Property of Radicals Examples

Slide 4

Examples:

Slide 5

Examples:

Slide 6

Quotient Property of Radicals

Slide 7

Examples:

Slide 8

Examples:

Slide 9

Rationalizing the denominator

Rationalizing the denominator means to remove any radicals from the denominator.

Ex: Simplify

Slide 10

Simplest Radical Form

No perfect nth power factors other than 1.

No fractions in the radicand.

No radicals in the denominator.

Slide 11

Examples:

Slide 12

Examples:

Slide 13

Adding radicals

We can only combine terms with radicals

if we have like radicals

Reverse of the Distributive Property

Slide 14

Examples:

Slide 15

Examples:

Slide 16

Multiplying radicals - Distributive Property

Slide 17

Multiplying radicals - FOIL

Slide 18

Examples:

Slide 19

Examples:

Slide 20

Conjugates

Slide 21

The product of conjugates is a rational number. Therefore, we can rationalize denominator of a fraction by multiplying by its conjugate.