Solving InequalitiesPage
1
1
Slide 1
1.6 Solving Inequalities
Slide 2
Solving Inequalities
Solving inequalities follows the same procedures as solving equations.
There are a few special things to
consider with inequalities:
We need to look carefully at the inequality sign.
We also need to graph the solution set.
Slide 3
Review of Inequality Signs
> greater than
< less than
greater than or equal
less than or equal
Slide 4
How to graph the solutions
> Graph any number greater than. . .
open circle, line to the right
< Graph any number less than. . .
open circle, line to the left
Graph any number greater than or equal to. . .
closed circle, line to the right
Graph any number less than or equal to. . .
closed circle, line to the left
Slide 5
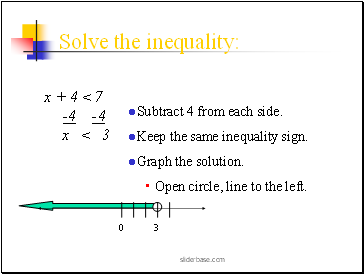
Solve the inequality:
x + 4 < 7
-4 -4
x < 3
Subtract 4 from each side.
Keep the same inequality sign.
Graph the solution.
Open circle, line to the left.
Slide 6
There is one special case.
Sometimes you may have to reverse the direction of the inequality sign!!
That only happens when you
multiply or divide both sides of the inequality by a negative number.
Slide 7
Example:
Solve: -3y + 5 >23
-5 -5
-3y > 18
-3 -3
y < -6
Subtract 5 from each side.
Divide each side by negative 3.
Reverse the inequality sign.
Graph the solution.
Open circle, line to the left.
Slide 8
Try these:
Solve 2x+3>x+5
Solve - c - 11>23
Solve 3(r-2)<2r+4
Contents
- Solving Inequalities
- Review of Inequality Signs
- How to graph the solutions
- Solve the inequality:
- There is one special case.
Last added presentations
- Buoyancy
- Sensory and Motor Mechanisms
- Simulation at NASA for the Space Radiation Effort
- Thermal Energy
- Heat-Energy on the Move
- Geophysical Concepts, Applications and Limitations
- Gravitation