The Copernican Revolution

Page
4

Slide 20

Mathematical perfection

The geometrical harmony in the heliocentric system (the distances between the planets) intrigued Kepler.

He found that the orbits of the 6 planets could be nested with the 5 known regular “perfect” solids.

Slide 21

The battle with Mars

Kepler worked for four years trying to derive the motions of Mars from Brahe’s observations

In the process, he discovered that the plane of the earth’s orbit and the plane of Mars’ (and eventually the other planets) passed through the sun

Suspecting the sun had a force over the planets, he investigated magnetism

While this is not true, it did lead him to the idea of elliptical orbits

“With reasoning derived from physical principles agreeing with experience, there is no figure left for the orbit of the planet except a perfect ellipse.”

Slide 22

Astronomia nova

Published in 1609, The New Astronomy was just that, it revolutionized the field

It predicted planetary positions as much as ten times better than previous models

It included physical causes for the movement of the planets

The ideas of the Greeks were gone – the heavens no longer were perfect, immutable, or different from the earth

Slide 23

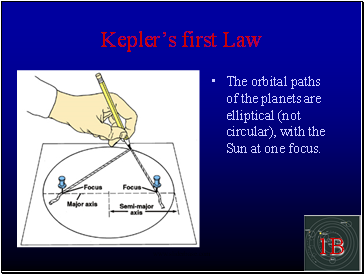
Kepler’s first Law

The orbital paths of the planets are elliptical (not circular), with the Sun at one focus.

Slide 24

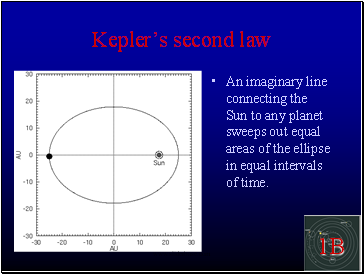
Kepler’s second law

An imaginary line connecting the Sun to any planet sweeps out equal areas of the ellipse in equal intervals of time.

Slide 25

Kepler’s Third Law

The square of a planet’s orbital period is proportional to the cube of its semi-major axis.

Slide 26

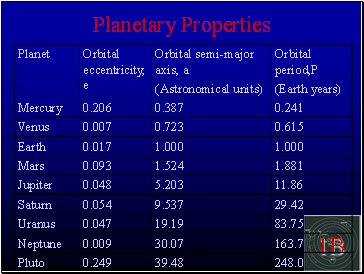
Planetary Properties

Slide 27

Other Solar System Bodies

Kepler derived his laws for the 6 planets known to him. The laws also apply to the 3 discovered planets and any other body orbiting the Sun (asteroids, comets, etc.)

Slide 28

A force for planetary motion

Newton proposes a force which controls the motion of the planets – GRAVITY

The larger the mass, the larger the force of gravity

The further the distance, the smaller the force of gravity