History of Modern Astronomy

Page
3

Slide 20

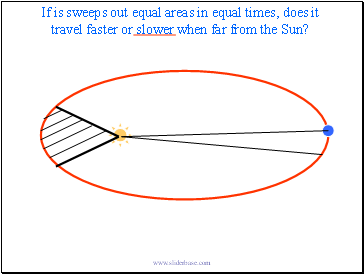
If is sweeps out equal areas in equal times, does it travel faster or slower when far from the Sun?

Slide 21

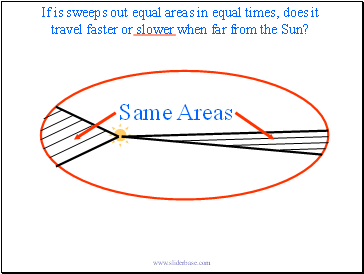
If is sweeps out equal areas in equal times, does it travel faster or slower when far from the Sun?

Slide 22

Kepler’s Third Law

Period of a planet, P

Average distance from the Sun (semimajor axis of ellipse), R

P2/R3 = 4p2/(G(m1+m2))

Approximately, P2earth/R3earth = P2planet/R3planet

Sometimes we use Earth-years and Earth-distance to the Sun (1 A.U.) as units.

The constant of proportionality depends on the mass of the Sun--and that’s how we know the mass of the Sun.

We can apply this to moons (or any satellite) orbiting a planet, and then the constant of proportionality depends on the mass of the planet.

Slide 23

Practice

While gazing at the planets that are visible with the naked eye, you tell a friend that the farther a planet is from the Sun, the longer its solar year is. Your friend first asks what a solar year is. After explaining that it’s the time required for a planet to return to its same position relative to the Sun, your friend then asks, “Why does it take longer for the outermost planets to orbit the Sun?” What is your reply?

Slide 24

Practice

What is the best method for determining the mass of Astronomical objects?

Kepler’s Third Law

For distant stars, this doesn’t work very well. Fortunately, there is a relationship between mass and brightness that will help us out.

Slide 25

Newton’s laws of motion

Newton’s first law

an object will have a constant velocity (constant speed, moving in a straight line) unless a net force acts on it

Newton’s second law

the acceleration of an object is proportional to the net force on the object divided by its mass

Newton’s third law

if object A exerts a force on object B, B exerts a force of equal magnitude back on A

Slide 26

Newton’s law of gravitation

mass attracts mass

the magnitude of the force of attraction is proportional to the product of their masses and the inverse of the square of the distance between them

mA

mB

ForceB on A

ForceA on B

Slide 27

Gravitational force and distance

If the bodies are twice as far apart, the gravitational force of each body on the other is 1/4 of their previous values.