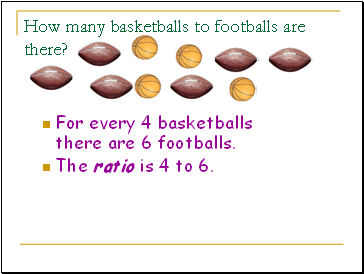Ratio

Page
1

Slide 1

DO NOW (not later):

Compare the number of boys to girls in the class.

Slide 2

The number of boys =

The number of girls =

If we compare boys to girls we get

_ boys to _ girls.

Slide 3

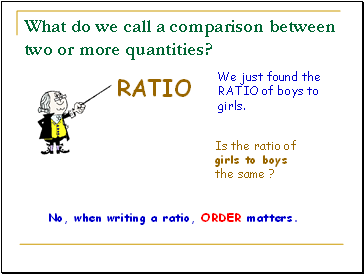
What do we call a comparison between two or more quantities?

RATIO

We just found the RATIO of boys to girls.

Is the ratio of girls to boys the same ?

No, when writing a ratio, ORDER matters.

Slide 4

AIM:

What is a ratio?

Slide 5

It’s Friday night and your friends are having a party……

The ratio of girls to guys is 2 to 12.

Would you want to attend the party?

Slide 6

How many basketballs to footballs are there?

For every 4 basketballs there are 6 footballs.

The ratio is 4 to 6.

Slide 7

What are some other ways we can write the ratio of basketball to footballs?

4 to 6

4 : 6

4

6

First quantity to Second quantity

First quantity : Second quantity

First quantity divided by the second quantity (as a fraction).

Every ratio can be written in 3 ways:

Careful!!

Order matters in a ratio.

4 to 6

Is NOT the same as

6 to 4

Slide 8

Write the ratio of sandwiches to coke bottles 3 different ways.

6:8 , 6 to 8, and 6

8

Since a fraction can be simplified, We can simplify the ratio 6/8 to 3/4. The ratio of sandwiches to coke bottles can also be expressed as 3 : 4 or 3 to 4.

In other words, ratios can be simplified to form equivalent ratios.

Slide 9

Equivalent Ratios

Simplify the following ratios:

4 to 8

10 to 8

8 to 10

Step 1 – Write the ratio as a fraction

Step 2 – Simplify the fraction (Find the greatest common factor (GCF) of both numbers and divide the numerator and denominator by the GCF).

Step 3 – Write the equivalent ratio in the same form as the question

= 4 / 4 = 1 = 1 to 2

8 8 / 4 2

GCF = 4

Slide 10

Equivalent Ratios can be formed by multiplying the ratio by any number.

For example, the ratio 2 : 3 can also be written as