Kinematic Equations NIS grade 11 physics review

Page
3

Slide 21

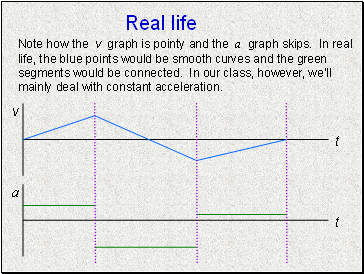
Real life

Note how the v graph is pointy and the a graph skips. In real life, the blue points would be smooth curves and the green segments would be connected. In our class, however, we’ll mainly deal with constant acceleration.

Slide 22

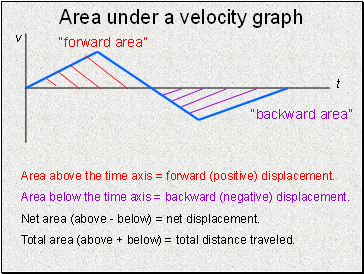
Area under a velocity graph

“forward area”

“backward area”

Area above the time axis = forward (positive) displacement.

Area below the time axis = backward (negative) displacement.

Net area (above - below) = net displacement.

Total area (above + below) = total distance traveled.

Slide 23

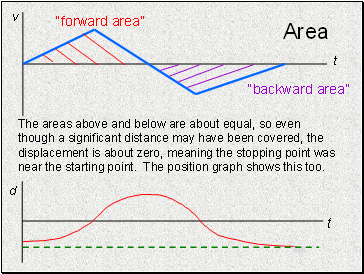
Area

The areas above and below are about equal, so even though a significant distance may have been covered, the displacement is about zero, meaning the stopping point was near the starting point. The position graph shows this too.

Slide 24

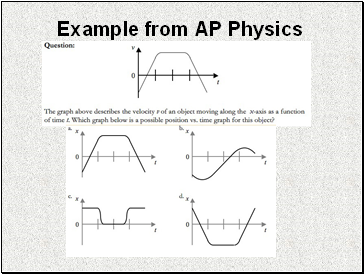
Example from AP Physics

Slide 25

Answer B Explained:

Slide 26

References:

http://www.thestudentroom.co.uk/wiki/Revision:Kinematics_-_Equations_of_Motion_for_Constant_Acceleration

https://www.csun.edu/science/credential/cset/cset-physics/ppt/kinematics-graphing.ppt

http://www.learnapphysics.com/index.html