Kinematic Equations NIS grade 11 physics review

Page
1

Slide 1

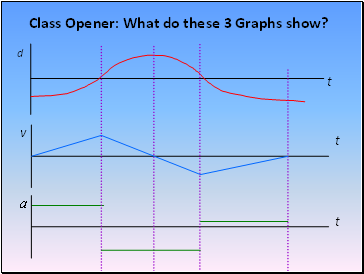
Class Opener: What do these 3 Graphs show?

Slide 2

Kinematic Equations

Kinematics is the study of objects in Motion

Grade 11 Physics

NIS, Taldykorgan

Mr. Marty

Slide 3

Objectives

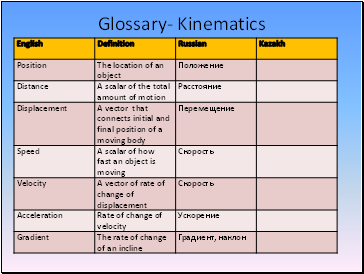
Recall the definitions of position, distance, displacement, speed, velocity and acceleration and distinguish whether these are scalars or vectors.

Use the equations of motion involving distance/displacement, speed/velocity, acceleration and time in calculations and in interpreting experimental results.

Plot and interpret DTVA Graphs distance-time, velocity-time and acceleration-time graphs calculating the area under velocity-time graph to work out distance travelled for motion with constant velocity or constant acceleration.

Slide 4

Glossary- Kinematics

Slide 5

Scalars and Vectors

Scalar is a quantity that has only magnitude

Vector is a quantity that has magnitude and direction

Examples:

distance

time

mass

speed

area

work

energy

pressure

Examples:

displacement

velocity

acceleration

force

momentum

electric field strength

Slide 6

Learners should know the equations

s = ½ (u+v)t

v = u +at

v2 = u2 +2as

s = ut + ½ at2

When 3 quantities are know the other 2 can be calculated

These equations only apply during constant acceleration (motion is one-dimensional motion with uniform acceleration).

When the acceleration is zero, s = ut.

Where:

s = final displacement (metres) u = initial velocity (metres per second, ms-1) v = final velocity (ms-1) a = acceleration (metres per second per second, ms-2) t = time taken (seconds, s)

Slide 7

Other symbols used in General Kinematic Equations

Final velocity: vf = v0 + a(t)

Distance traveled: d = v0 t + (½)at2

(Final velocity)2: vf2= (v0 t)2 + 2ad

Distance traveled: d = [(v0 + vf)/2]*t

Slide 8

Calculus formulas

Acceleration is the second derivative of displacement and velocity is the first derivative of displacement

Integration will

give the area under a curve

Slide 9

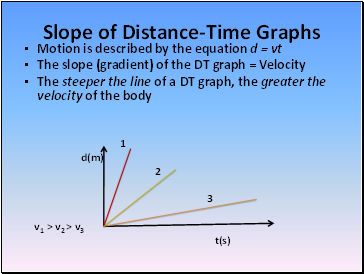
Slope of Distance-Time Graphs