Pythagorean Theorum Revised

Page
1

Slide 1

The Pythagorean Theorem Mr. Clutter VMS Library

Slide 2

Pythagoras

Lived in southern Italy during the sixth century B.C.

Considered the first true mathematician

Used mathematics as a means to understand the natural world

First to teach that the earth was a sphere that revolves around the sun

Slide 3

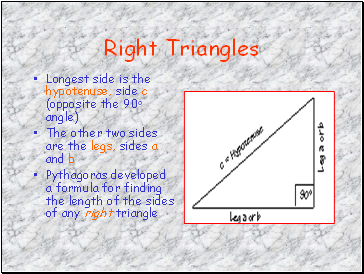
Right Triangles

Longest side is the hypotenuse, side c (opposite the 90o angle)

The other two sides are the legs, sides a and b

Pythagoras developed a formula for finding the length of the sides of any right triangle

Slide 4

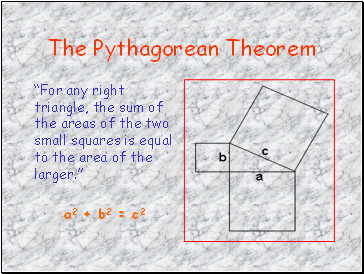
The Pythagorean Theorem

“For any right triangle, the sum of the areas of the two small squares is equal to the area of the larger.”

a2 + b2 = c2

Slide 5

Proof

Slide 6

Applications

The Pythagorean theorem has far-reaching ramifications in other fields (such as the arts), as well as practical applications.

The theorem is invaluable when computing distances between two points, such as in navigation and land surveying.

Another important application is in the design of ramps. Ramp designs for handicap-accessible sites and for skateboard parks are very much in demand.

Slide 7

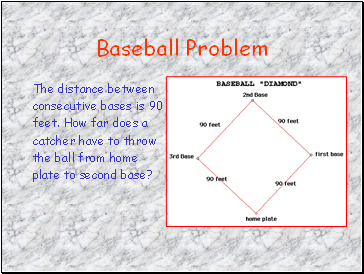
Baseball Problem

A baseball “diamond” is really a square.

You can use the Pythagorean theorem to find distances around a baseball diamond.

Slide 8

Baseball Problem

The distance between

consecutive bases is 90

feet. How far does a

catcher have to throw

the ball from home

plate to second base?

Slide 9

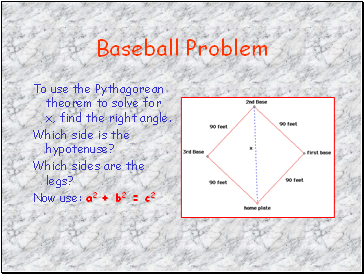
Baseball Problem

To use the Pythagorean theorem to solve for x, find the right angle.

Which side is the hypotenuse?

Which sides are the legs?

Now use: a2 + b2 = c2

Slide 10

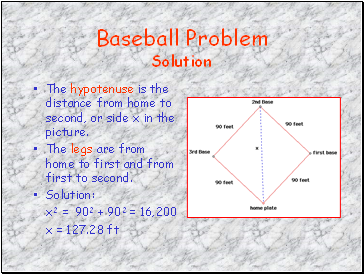
Baseball Problem Solution

The hypotenuse is the distance from home to second, or side x in the picture.

The legs are from home to first and from first to second.

Solution:

x2 = 902 + 902 = 16,200

x = 127.28 ft

Slide 11

Ladder Problem