Early Greek Science and Philosophy

Page
3

“The psychological conditions which make a society or an epoch creative and consistently original have been little studied, but it seems likely that social conditions analogous to those seen in individual creativity are important. Freedom of expression and movement, lack of fear of dissent and contradiction, a willingness to break with custom, a spirit of play as well as of dedication to work, purpose on a grand scale; these are some of the attributes which a creative social entity, whether vast or tiny, can be expected to have.”

— Frank Barron, Institute of Personality Assessment and Research, University of California, Berkeley

Slide 15

Thank You

Slide 16

Fibonacci Series:

Rabbit Breeding

Slide 17

“While studying the of how many rabbits will be born from an original pair of rabbits, assuming that every month each pair produces another pair and that rabbits begin to breed when they are two months old. After the process got started, the total number of pairs of rabbits at the end of each month would be as follows: 1, 2, 3, 5, 8, 13, 21, 55, 89, 144, 233. Each successive number is the sum of the two preceding numbers. The Fibonacci series is a lot more than a source of amusement. Divide any of the Fibonacci numbers by the next higher number [and] the sequence of ratios will converge to 0.618. Dividing a number by its previous number will converge to 1.618. The Greeks knew this proportion and called it the ‘Golden Mean’.

– Peter L. Bernstein, Against the Gods, 1996, XXVI

Slide 18

Fibonacci Numbers

Slide 19

Pythagoras

Golden Mean, Rectangles and Triangles

Slide 20

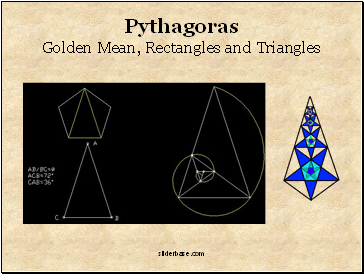
Pythagoras Golden Mean, Rectangles and Triangles

Slide 21

“The familiar-looking spiral [with areas based on the Fibonacci series] appears in the shape of certain galaxies, in a ram’s horn, in many seashells, and in the coil of the ocean waves that surfers ride. The structure maintains its form without change as it is made larger and larger and regardless of the size of the initial square with which the process is launches: form is independent of growth. The journalist William Hoffer has remarked, ‘The great golden spiral seems to be nature’s way of building quantity without sacrificing quality.’”

– Peter L. Bernstein, Against the Gods, 1996, XXVIII