Functions

Page
1

Slide 1

Functions

sliderbase.com

Slide 2

Definition and notation

Definition: A function f from a set X to a set Y

is a relationship between elements of X and Y

with the property that

each element of X is related to a unique element of Y.

Denoted f:X→Y .

X is called domain of f; Y is called co-domain of f.

Example: X=Z, Y=Z and f : x → 2∙x / 2

xX ! yY such that f(x)=y .

f(x) is called f of x (or image of x under f).

Range of f = {yY | y=f(x) for some x in X}

Inverse image of y = {xX | f(x)=y}

Example(cont.): range of f = all even integers ;

inverse image of 4 = {3, 4} .

sliderbase.com

Slide 3

Examples of Functions

Squaring function: f : x → x2 .

Constant function: f : x → 3 .

Linear function: f : x → 3x+2 .

Factorial function: f : n → n! .

Any sequence can be considered

as a function defined on a set of integers.

E.g., sequence 2,5,8,11,14,…

is a function from Z+ to Z+

defined as follows f : n → 3n-1

sliderbase.com

Slide 4

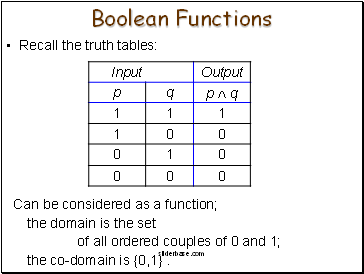
Boolean Functions

Recall the truth tables:

Can be considered as a function;

the domain is the set

of all ordered couples of 0 and 1;

the co-domain is {0,1} .

sliderbase.com

Slide 5

Boolean Functions

Definition:

An (n-place) Boolean function is a function

whose domain

is the set of all ordered n-tuples of 0’s and 1’s

and whose co-domain

is the set {0,1}.

Example: f : (x,y,z) → (~x  y)  z

sliderbase.com

Slide 6

One-to-one Functions

Definition:

Let F be a function from set X to set Y.

F is one-to-one (or injective) iff

for all elements x1, x2  X

if F(x1)=F(x2) then x1=x2 .

Examples: Define f : Z → Z by f(n)=2n+3 ;

g : R → R by f(x)=x2 .

Then f is one-to-one, and g is not.

sliderbase.com

Slide 7

Onto Functions

Definition:

Let F be a function from set X to set Y.

F is onto (or surjective) iff

for any element y  Y there is a x X

such that F(x)=y .

Examples: Define f : Z → Z by f(n)=2n+3 ;

g : Z → Z by f(n)=n-2 .