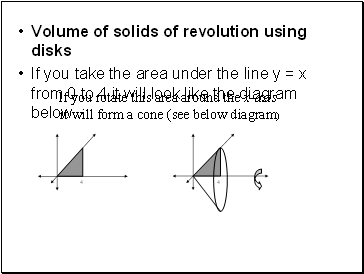Calculus Notes

Page
1

Slide 1

Calculus Notes Ch 6.2

Volumes by slicing can be found by adding up each slice of the solid as the thickness of the slices gets

smaller and smaller, in other words

the number of slices goes to infinity.

To find the volume of each slice of the pyramid you would find the area of each square then multiply the area by the thickness of the slice. The thickness would be dx because we are slicing with respect to the x-axis. Next you would add the volumes of each slice together to find the total volume.

This would be a Riemann sum with the limit as n the number of slices going to infinity.

Slide 2

Remember the from Ch 5.5

Only now instead of f(x*) we will be summing the areas of the base of each slice. So change f(x*)in the Riemann Sum to A(x*)which represents the area of the base.

Slide 3

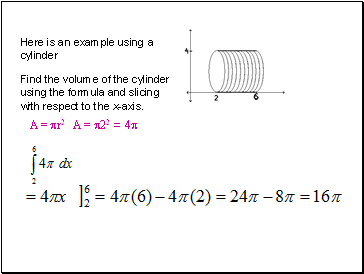
Here is an example using a cylinder

Find the volume of the cylinder using the formula and slicing with respect to the x-axis.

A = r2 A = 22 = 4

Slide 4

Now use the formula you learned in Geometry to find the area

V= r2 h=(22)(4) = 16 

You can also work problems like these with respect to the y-axis.

Slide 5

Volume of solids of revolution using disks

If you take the area under the line y = x from 0 to 4 it will look like the diagram below

If you rotate this area around the x-axis

it will form a cone (see below diagram)

Slide 6

Now use the formula below to find the volume of the 3-D figure formed by rotating around the x-axis.

http://www.plu.edu/~heathdj/java/calc2/Solid.html

This method is called disks when revolved around the x-axis ( note: it is sliced with respect to the x-axis and is revolved around the x-axis)

Slide 7

Formula for finding the volume of the solid formed when f(x) is revolved around the x-axis

Each slice is a circle, the formula for the area of a circle is A= r2. The radius is the y-value of the function AKA f(x). So, the area formula becomes A= (f(x))2

Substitute into the formula

Slide 8

Equation y = x from 0 to 4

With geometry V = 1/3  (42)(4)=64/3

With Calculus

Slide 9