Quadratic Functions

Page
2

3. If k is odd, the graph crosses the x-axis at x = a.

Repeated Roots (Zeros)

Slide 13

Intermediate Value Theorem

If a < b are two real numbers

and f (x)is a polynomial function

with f (a)  f (b),

then f (x) takes on every real

number value between

f (a) and f (b) for a  x  b.

Slide 14

NOTE to Intermediate Value

Let f (x) be a polynomial function and a < b be two real numbers.

If f (a) and f (b)

have opposite signs

(one positive and one negative),

then f (x) = 0 for a < x < b.

Slide 15

Polynomial and

Synthetic Division

Dr. Claude S. Moore Danville Community College

PRECALCULUS I

Slide 16

Full Division Algorith

If f (x) and d(x) are polynomials with d(x)  0 and the degree of d(x) is less than or equal to the degree of f(x), then q(x) and r (x) are unique polynomials such that f (x) = d(x) ·q(x) + r (x) where r (x) = 0 or has a degree less than d(x).

Slide 17

Short Division Algorith

f (x) = d(x) ·q(x) + r (x)

dividend quotient divisor remainder

where r (x) = 0 or has a degree less than d(x).

Slide 18

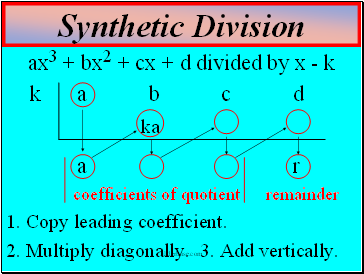
Synthetic Division

ax3 + bx2 + cx + d divided by x - k

k a b c d

ka

a r

coefficients of quotient remainder

1. Copy leading coefficient.

2. Multiply diagonally. 3. Add vertically.

Slide 19

Remainder Theorem

If a polynomial f (x)

is divided by x - k,

the remainder is r = f (k).

Slide 20

Factor Theorem

A polynomial f (x)

has a factor (x - k)

if and only if f (k) = 0.

Slide 21

Real Zeros of Polynomial Functions

Dr. Claude S. Moore Danville Community College

PRECALCULUS I

Slide 22

Descartes’s Rule of Signs

a’s are real numbers, an 0, and a0 0.

1. Number of positive real zeros of f equals number of variations in sign of f(x), or less than that number by an even integer.

2. Number of negative real zeros of f equals number of variations in sign of f(-x), or less than that number by an even integer.