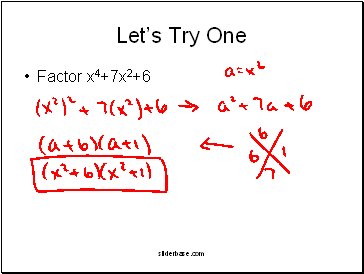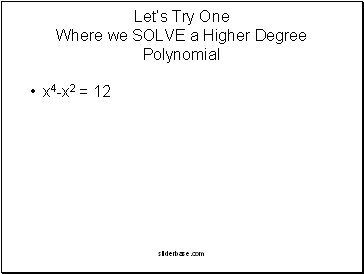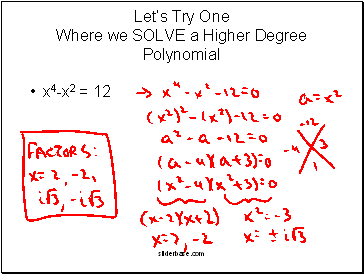Solving Polynomial Equations

Page
2

Let’s Try One

81x3-192=0

Slide 13

Factor by Using a Quadratic Form

Ex: x4-2x2-8

Since this equation has the form of a quadratic expression, we can factor it like one. We will make temporary substitutions for the variables

= (x2)2 – 2(x2) – 8

Substitute a in for x2

= a2 – 2a – 8

This is something that we can factor

(a-4)(a+2)

Now, substitute x2 back in for a

(x2-4)(x2+2)

(x2-4) can factor, so we rewrite it as (x-2)(x+2)

So, x4-2x2-8 will factor to (x-2)(x+2)(x2+2)

Slide 14

Let’s Try One

Factor x4+7x2+6

Slide 15

Let’s Try One

Factor x4+7x2+6

Slide 16

Let’s Try One Where we SOLVE a Higher Degree Polynomial

x4-x2 = 12

Slide 17

Let’s Try One Where we SOLVE a Higher Degree Polynomial

x4-x2 = 12