The Remainder and Factor Theorems

Page
2

4 2 –4 –7 –13 –10

8 16 36 92

2 4 9 23 82

Slide 10

The Factor Theorem

The binomial (x – a) is a factor of the

polynomial f(x) if and only if f(a) = 0.

Slide 11

The Factor Theorem

When a polynomial is divided by one of its

binomial factors, the quotient is called a

depressed polynomial.

If the remainder (last number in a depressed

polynomial) is zero, that means f(#) = 0. This

also means that the divisor resulting in a

remainder of zero is a factor of the polynomial.

Slide 12

The Factor Theorem

x3 + 4x2 – 15x – 18

x – 3

3 1 4 –15 –18

3 21 18

1 7 6 0

Since the remainder is zero, (x – 3) is a factor of

x3 + 4x2 – 15x – 18.

This also allows us to find the remaining factors of

the polynomial by factoring the depressed polynomial.

Slide 13

The Factor Theorem

x3 + 4x2 – 15x – 18

x – 3

3 1 4 –15 –18

3 21 18

1 7 6 0

x2 + 7x + 6

(x + 6)(x + 1)

The factors of

x3 + 4x2 – 15x – 18

are

(x – 3)(x + 6)(x + 1).

Slide 14

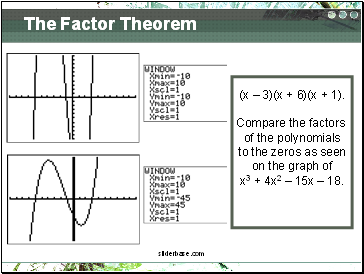
The Factor Theorem

(x – 3)(x + 6)(x + 1).

Compare the factors

of the polynomials

to the zeros as seen

on the graph of

x3 + 4x2 – 15x – 18.

Slide 15

The Factor Theorem

Given a polynomial and one of its factors, find the remaining

factors of the polynomial. Some factors may not be binomials.

x3 – 11x2 + 14x + 80

x – 8

2. 2x3 + 7x2 – 33x – 18

x + 6

(x – 8)(x – 5)(x + 2)

(x + 6)(2x + 1)(x – 3)