Polarization of Light from Basics to Instruments

Page
3

Part II: Stokes parameters

Slide 23

Stokes vector

The Stokes parameters can be arranged in a Stokes vector:

Linear polarization

Circular polarization

Fully polarized light

Partially polarized light

Unpolarized light

Part II: Stokes parameters, Stokes vectors

Slide 24

Pictorial representation of the Stokes parameters

Part II: Stokes parameters

Slide 25

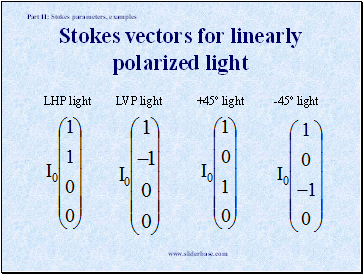
Stokes vectors for linearly polarized light

LHP light

LVP light

+45º light

-45º light

Part II: Stokes parameters, examples

Slide 26

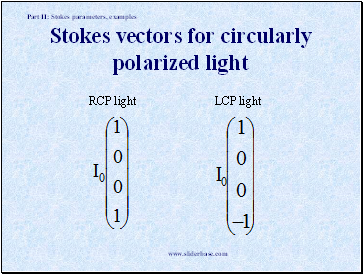
Stokes vectors for circularly polarized light

RCP light

LCP light

Part II: Stokes parameters, examples

Slide 27

(Q,U) to (P,)

In the case of linear polarization (V=0):

Part II: Stokes parameters

Slide 28

Mueller matrices

If light is represented by Stokes vectors, optical components are then described with Mueller matrices:

[output light] = [Muller matrix] [input light]

Part II: Stokes parameters, Mueller matrices

Slide 29

Mueller calculus (I)

Element 1 Element 2 Element 3

I’ = M3 M2 M1 I

Part II: Stokes parameters, Mueller matrices

Slide 30

Mueller calculus (II)

Mueller matrix M’ of an optical component with Mueller matrix M rotated by an angle :

M’ = R(- ) M R() with:

Part II: Stokes parameters, Mueller matrices

Slide 31

Jones formalism

Stokes vectors and Mueller matrices cannot describe interference effects. If the phase information is important (radio-astronomy, masers .), one has to use the Jones formalism, with complex vectors and Jones matrices:

Jones vectors to describe the polarization of light:

Jones matrices to represent optical components:

BUT: Jones formalism can only deal with 100% polarization .

Part II: Stokes parameters, Jones formalism, not that important here .

Slide 32

Optical components for polarimetry

Complex index of refraction

Polarizers

Retarders

Slide 33