AreaPage
1
1
Slide 1
AP Calculus
Area
Slide 2
Area of a Plane Region
Calculus was built around two problems
Tangent line
Area
Slide 3
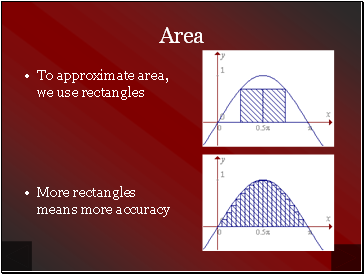
Area
To approximate area, we use rectangles
More rectangles means more accuracy
Slide 4
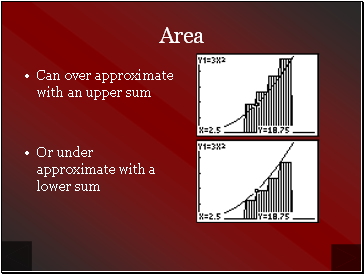
Area
Can over approximate with an upper sum
Or under approximate with a lower sum
Slide 5
Area
Variables include
Number of rectangles used
Endpoints used
Slide 6
Area
Regardless of the number of rectangles or types of inputs used, the method is basically the same.
Multiply width times height and add.
Slide 7
Upper and Lower Sums
An upper sum is defined as the area of circumscribed rectangles
A lower sum is defined as the area of inscribed rectangles
The actual area under a curve is always between these two sums or equal to one or both of them.
Slide 8
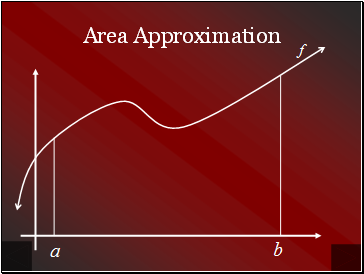
Area Approximation
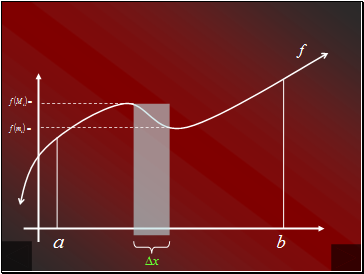
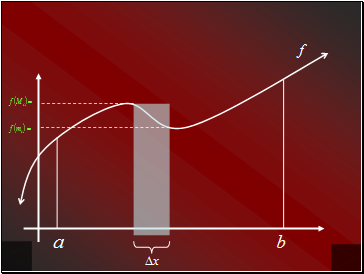
We wish to approximate the area under a curve f from a to b.
We begin by subdividing the interval [a, b] into n subintervals.
Each subinterval is of width .
Slide 9
Area Approximation
Slide 10
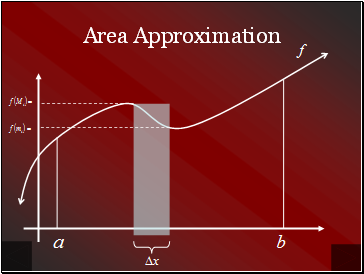
Area Approximation
We wish to approximate the area under a curve f from a to b.
We begin by subdividing the interval [a, b] into n
subintervals of width .
Minimum value of f in the ith subinterval
Maximum value of f in the ith subinterval
Slide 11
Area Approximation
Slide 12
Area Approximation
So the width of each rectangle is
Slide 13
Slide 14
So the width of each rectangle is
The height of each rectangle is either
or
Area Approximation
Slide 15
1 2
Contents
Last added presentations
- Heat-Energy on the Move
- Newton’s Law of Gravity
- Radioactivity and Nuclear Reactions
- Madame Marie Curie
- Newton’s third law of motion
- Space Radiation
- Motion