Mathematical Proof

Page
1

Slide 1

CORE 1 proof

Slide 2

What is Mathematical Proof?

The process of starting with an assumption, or a statement which is given, and, by using logical argument, arriving at a conclusion

Slide 3

Mathematical Proof

‘Prove that …’ or ‘Given …, prove …’ or ‘ Prove …, given …’

Form a logical argument

Start with what is given or standard results

Deduce each step from previous

Standard results can be used at any stage

Slide 4

Mathematical statements

ΔABC is isosceles

sinθ = ¾

The gradient of y=mx+c is m

Slide 5

Implication Signs

Use to express the relationship between statements

implies

does not imply

is implied by

implies and is implied by

Slide 6

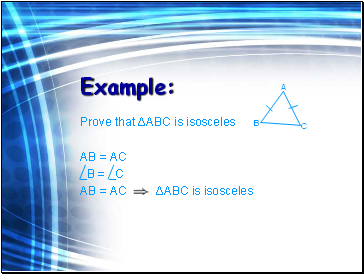
Example:

Prove that ΔABC is isosceles

AB = AC

‗B = _C

AB = AC ΔABC is isosceles

A

B

C

Slide 7

Example:

Link the statements a = 0 and ab = 0 using implication signs.

a = 0 ab = 0

ab = 0 a = 0 (b could be 0)

ab = 0 Either a = 0 or b = 0

Slide 8

Example:

Slide 9

Slide 10

Example:

Prove that sum of an even number and an odd number is always odd.

Slide 11

Let 2n be any even number, where n is an integer.

2m + 1 be any odd number, where m is an integer.

2n + 2m + 1 = 2(n+m) + 1

n+m is an integer

n+m is an integer

2(n+m) is even

2(n+m) + 1 is odd

2(n+m) + 1 = 2n + 2m + 1

the sum of an even number and an odd number is always odd.