Introduction to Oscillations and Simple Harmonic Motion

Page
2

Slide 9

The period and frequency of a wave

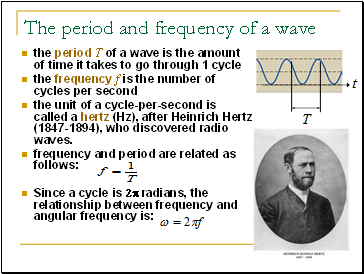
the period T of a wave is the amount of time it takes to go through 1 cycle

the frequency f is the number of cycles per second

the unit of a cycle-per-second is called a hertz (Hz), after Heinrich Hertz (1847-1894), who discovered radio waves.

frequency and period are related as follows:

Since a cycle is 2p radians, the relationship between frequency and angular frequency is:

Slide 10

10

Example: 1

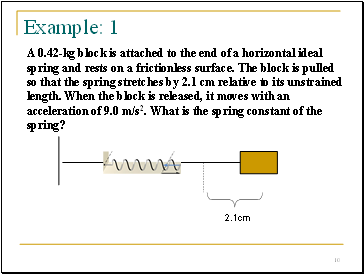
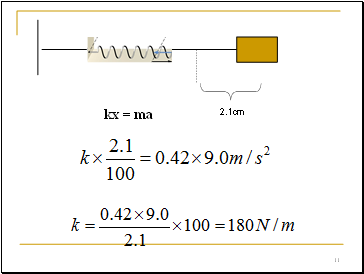
A 0.42-kg block is attached to the end of a horizontal ideal spring and rests on a frictionless surface. The block is pulled so that the spring stretches by 2.1 cm relative to its unstrained length. When the block is released, it moves with an acceleration of 9.0 m/s2. What is the spring constant of the spring?

Slide 11

11

kx = ma

Slide 12

Energy and Simple Harmonic Motion

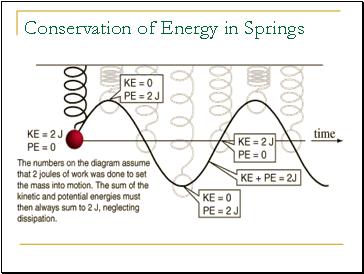
A spring also has potential energy when the spring is stretched or compressed, which we refer to as elastic potential energy. Because of elastic potential energy, a stretched or compressed spring can do work on an object that is attached to the spring.

Slide 13

Definition of elastic potential energy

The elastic potential energy PEelastic is the energy that a spring has by virtue of being stretched or compressed. For an ideal spring that has a spring constant k and is stretched or compressed by an amount x relative to its unstrained length, the elastic potential energy is

SI Unit of Elastic Potential Energy: joule (J)

Slide 14

Conservation of Energy in Springs

Slide 15

Example 2:

A 200 g mass is attached to a spring and executes simple harmonic motion with a period of 0.25 s If the total energy of the system is 2.0 J, find the (a) force constant of the spring (b) the amplitude of the motion

126.3 N/m

0.18 m

Slide 16

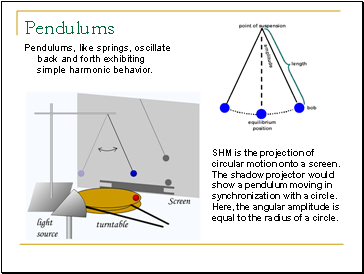
Pendulums

Pendulums, like springs, oscillate back and forth exhibiting simple harmonic behavior.

SHM is the projection of circular motion onto a screen. The shadow projector would show a pendulum moving in synchronization with a circle. Here, the angular amplitude is equal to the radius of a circle.

Slide 17

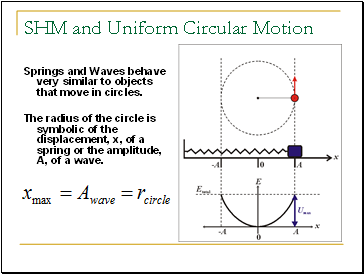
SHM and Uniform Circular Motion