Introduction to Oscillations and Simple Harmonic Motion

Page
1

Slide 1

Introduction to Oscillations and Simple Harmonic Motion

Taldykorgan, KZ

NIS Grade 11 Physics

Slide 2

Objectives

Describe examples of free oscillations.

Describe the conditions of Simple Harmonic Motion.

Apply Hooke’s Law for objects moving with simple harmonic motion.

Describe the motion of pendulums and calculate the length required to produce a given frequency.

Slide 3

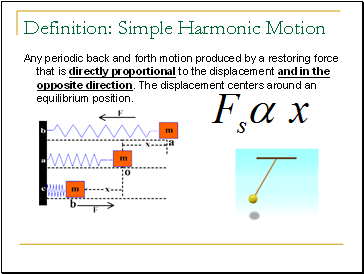
Definition: Simple Harmonic Motion

Any periodic back and forth motion produced by a restoring force that is directly proportional to the displacement and in the opposite direction. The displacement centers around an equilibrium position.

Slide 4

4

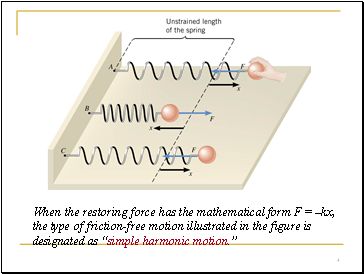
When the restoring force has the mathematical form F = –kx, the type of friction-free motion illustrated in the figure is designated as “simple harmonic motion.”

Slide 5

Springs – Hooke’s Law

One of the simplest type of simple harmonic motion is called Hooke's Law. This is primarily in reference to SPRINGS.

The negative sign only tells us that “F” is what is called a RESTORING FORCE, in that it works in the OPPOSITE direction of the displacement.

Slide 6

6

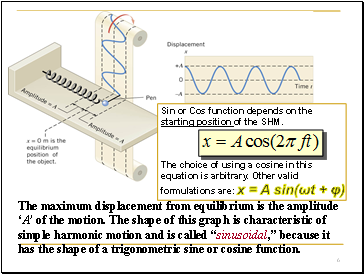
The maximum displacement from equilibrium is the amplitude ‘A’ of the motion. The shape of this graph is characteristic of simple harmonic motion and is called “sinusoidal,” because it has the shape of a trigonometric sine or cosine function.

Sin or Cos function depends on the starting position of the SHM.

The choice of using a cosine in this equation is arbitrary. Other valid formulations are: x = A sin(ωt + φ)

Slide 7

Springs are like Waves and Circles

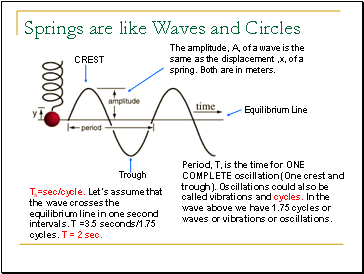
The amplitude, A, of a wave is the same as the displacement ,x, of a spring. Both are in meters.

CREST

Trough

Equilibrium Line

Period, T, is the time for ONE COMPLETE oscillation (One crest and trough). Oscillations could also be called vibrations and cycles. In the wave above we have 1.75 cycles or waves or vibrations or oscillations.

Ts=sec/cycle. Let’s assume that the wave crosses the equilibrium line in one second intervals. T =3.5 seconds/1.75 cycles. T = 2 sec.

Slide 8

Frequency

The FREQUENCY of a wave is the inverse of the PERIOD. That means that the frequency is the number of cycles per sec. The commonly used unit is HERTZ (Hz).