Atomic Structure

Page
4

Slide 17

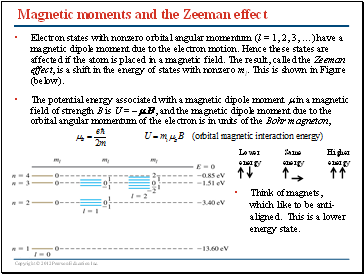
Magnetic moments and the Zeeman effect

Electron states with nonzero orbital angular momentum (l = 1, 2, 3, …) have a magnetic dipole moment due to the electron motion. Hence these states are affected if the atom is placed in a magnetic field. The result, called the Zeeman effect, is a shift in the energy of states with nonzero ml. This is shown in Figure (below).

The potential energy associated with a magnetic dipole moment m in a magnetic field of strength B is U = -mB , and the magnetic dipole moment due to the orbital angular momentum of the electron is in units of the Bohr magneton,

Think of magnets, which like to be anti-aligned. This is a lower energy state.

Slide 18

Zeeman Effect (Sunspots)

Slide 19

Zeeman Effect (Sunspots)

Slide 20

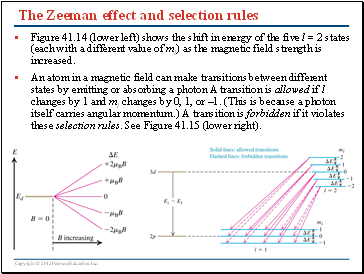
The Zeeman effect and selection rules

Figure 41.14 (lower left) shows the shift in energy of the five l = 2 states (each with a different value of ml) as the magnetic field strength is increased.

An atom in a magnetic field can make transitions between different states by emitting or absorbing a photon A transition is allowed if l changes by 1 and ml changes by 0, 1, or –1. (This is because a photon itself carries angular momentum.) A transition is forbidden if it violates these selection rules. See Figure 41.15 (lower right).

Slide 21

The anomalous Zeeman effect and electron spin

For certain atoms the Zeeman effect does not follow the simple pattern that we have described (see Figure 41.16 below). This is because an electron also has an intrinsic angular momentum, called spin angular momentum.

Slide 22

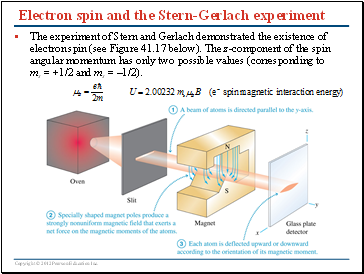
Electron spin and the Stern-Gerlach experiment

The experiment of Stern and Gerlach demonstrated the existence of electron spin (see Figure 41.17 below). The z-component of the spin angular momentum has only two possible values (corresponding to ms = +1/2 and ms = –1/2).

Slide 23

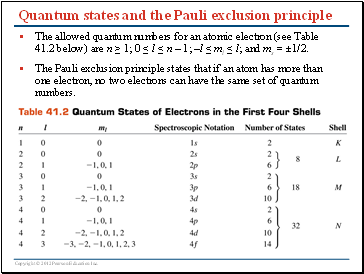
Quantum states and the Pauli exclusion principle

The allowed quantum numbers for an atomic electron (see Table 41.2 below) are n ≥ 1; 0 ≤ l ≤ n – 1; –l ≤ ml ≤ l; and ms = ±1/2.

The Pauli exclusion principle states that if an atom has more than one electron, no two electrons can have the same set of quantum numbers.

Slide 24

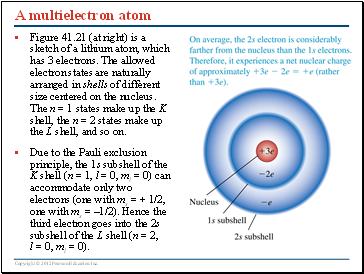
A multielectron atom