Hipparchus

Page
1

Slide 1

Claudius Ptolemy

Saving the Heavens

Slide 2

Euclid’s Elements at work

Euclid’s Elements quickly became the standard text for teaching mathematics at the Museum at Alexandria.

Philosophical questions about the world could now be attacked with exact mathematical reasoning.

Slide 3

Eratosthenes of Cyrene

276 - 194 BCE

Born in Cyrene, in North Africa (now in Lybia).

Studied at Plato’s Academy.

Appointed Librarian at the Museum in Alexandria.

Slide 4

“Beta”

Eratosthenes was prolific. He worked in many fields. He was a:

Poet

Historian

Mathematician

Astronomer

Geographer

He was nicknamed “Beta.”

Not the best at anything, but the second best at many things.

Slide 5

Eratosthenes’ Map

He coined the word “geography” and drew one of the first maps of the world (above).

Slide 6

Using Euclid

Eratosthenes made very clever use of a few scant observations, plus a theorem from Euclid to decide one of the great unanswered questions about the world.

Slide 7

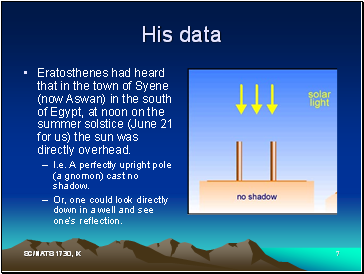
His data

Eratosthenes had heard that in the town of Syene (now Aswan) in the south of Egypt, at noon on the summer solstice (June 21 for us) the sun was directly overhead.

I.e. A perfectly upright pole (a gnomon) cast no shadow.

Or, one could look directly down in a well and see one’s reflection.

Slide 8

His data, 2

Based on reports from on a heavily travelled trade route, Eratosthenes calculated that Alexandria was 5000 stadia north of Syene.

Syene

5000 stadia

Slide 9

His data, 3

Eratosthenes then measured the angle formed by the sun’s rays and the upright pole (gnomon) at noon at the solstice in Alexandria. (Noon marked by when the shadow is shortest.)

The angle was 7°12’.

Slide 10

Proposition I.29 from Euclid

A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the interior angles on the same side equal to two right angles.