Hipparchus

Page
2

Slide 11

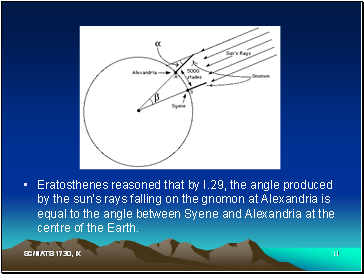
Eratosthenes reasoned that by I.29, the angle produced by the sun’s rays falling on the gnomon at Alexandria is equal to the angle between Syene and Alexandria at the centre of the Earth.

Slide 12

Calculating the size of the Earth

The angle at the gnomon, α, was 7°12’, therefore the angle at the centre of the Earth, β, was is also 7°12’ which is 1/50 of a complete circle.

Therefore the circumference of the Earth had to be stadia = 250,000 stadia.

7°12’ x 50 = 360°

50 x 5000 = 250,000

Slide 13

Eratosthenes’ working assumptions

1. The Sun is very far away, so any light coming from it can be regarded as traveling in parallel lines.

2. The Earth is a perfect sphere.

3. A vertical shaft or a gnomon extended downwards will pass directly through the center of the Earth.

4. Alexandria is directly north of Syene, or close enough for these purposes.

Slide 14

A slight correction

Later Eratosthenes made a somewhat finer observation and calculation and concluded that the circumference was 252,000 stadia.

So, how good was his estimate.

It depends….

Slide 15

What, exactly, are stadia?

Stadia are long measures of length in ancient times.

A stade (singular of stadia) is the length of a stadium.

And that was…?

Slide 16

Stadium lengths

In Greece the typical stadium was 185 metres.

In Egypt, where Eratosthenes was, the stade unit was 157.5 metres.

Slide 17

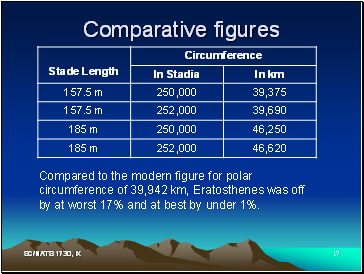
Comparative figures

Compared to the modern figure for polar circumference of 39,942 km, Eratosthenes was off by at worst 17% and at best by under 1%.

Slide 18

An astounding achievement

Eratosthenes showed that relatively simple mathematics was sufficient to determine answers to many of the perplexing questions about nature.

Slide 19

Hipparchus of Rhodes

Hipparchus of Rhodes

Became a famous astronomer in Alexandria.

Around 150 BCE developed a new tool for measuring relative distances of the stars from each other by the visual angle between them.

Slide 20

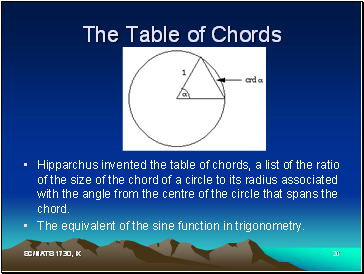
The Table of Chords