The Milky Way Galaxy

Page
3

Pop I young and metal rich

Pop II old and metal poor

Since most stars are smaller than the sun, the Milky Way actually contains far more than 23 billion stars – more like 200 billion

Morphology of our Galaxy

Disk – mainly Pop I

Halo – mainly Pop II

Bulge – mix of Pop I and II

Slide 13

Differential Rotation

Everything in the Galaxy orbits around the Galactic center

Material closer to the center travels on faster orbits (takes less time to make one full orbit)

Similar to the way the planets orbit the Sun

Orbital periods at different distances from the Galactic center can tell us the distribution of mass in the Galaxy

Examining motions of stars in the disk are most helpful for mapping the distribution of mass

Slide 14

M(R) = 0R (r) dV

Motion at distance R from center depends only on M(R)

That mass behaves as if it were centrally concentrated

For an object with mass m at R, gravity must balance acceleration of circular motion

GM(R)m/R2 = mv2/R

M(R) = v(R)2R/G

Measure v(R) and get M(R)

Let ω(R) = v(R)/R, then

M(R) = ω(R)2R3/G

v(R) or ω(R) gives the rotation curve of the Galaxy.

v

m

M

R

Differential Rotation

Slide 15

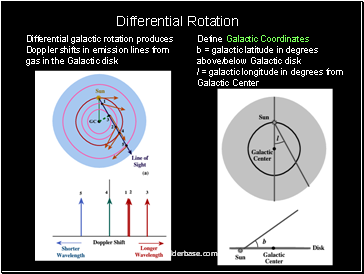
Differential galactic rotation produces Doppler shifts in emission lines from gas in the Galactic disk

Differential Rotation

Slide 16

Use cylindrical coordinates for the Galactic plane to define the Sun’s motion w.r.t the Local Standard of Rest

The Sun (and most stars) are on slightly perturbed orbits that resemble rosettes making it difficult to measure relative motions of stars around the Sun.

Establish a reference frame that is a perfect circular orbit about the Galactic Center.

Local Standard of Rest - reference frame for measuring velocities in the Galaxy.

Position of the Sun if its motion were completely governed by circular motion around the Galaxy.

Local Standard of Rest

Slide 17

To determine the Suns motion wrt to LSR, we observe the average motions of all stars in the Sun’s vicinity and measure the following:

Π - Πo = U (speed away from GC) = -10.4 km/s [7.5 +/-1 km/s]

Z - Zo = W (speed towards NGP) = 7.3 km/s [6.8 (+/- 0.1) km/s]

Θ - Θo = V (speed in direction of motion) = V = 14.8 km/s [13.5 (+/- 3) km/s]

The Sun is moving toward the Galactic center, faster than the LSR, and northward toward the NGP. Net motion is 19.5 km/s in the direction of constellation Hercules