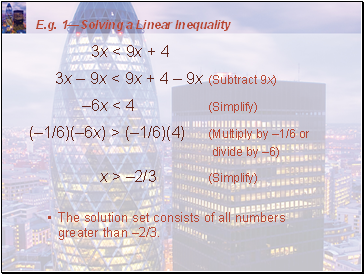College Algebra

Page
1

Slide 1

College Algebra

Fifth Edition

James Stewart  Lothar Redlin  Saleem Watson

Slide 2

Equations and Inequalities

1

Slide 3

Inequalities

1.6

Slide 4

Inequalities

Some problems in algebra lead to inequalities instead of equations.

An inequality looks just like an equation—except that, in the place of the equal sign is one of these symbols: <, >, ≤, or ≥.

Here is an example: 4x + 7 ≤ 19

Slide 5

Inequalities

The table shows that some numbers satisfy the inequality and some numbers don’t.

Slide 6

Solving Inequalities

To solve an inequality that contains a variable means to find all values of the variable that make the inequality true.

Unlike an equation, an inequality generally has infinitely many solutions.

These form an interval or a union of intervals on the real line.

Slide 7

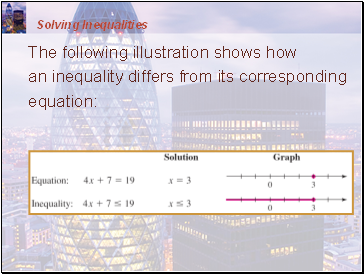
Solving Inequalities

The following illustration shows how an inequality differs from its corresponding equation:

Slide 8

Solving Inequalities

To solve inequalities, we use the following rules to isolate the variable on one side of the inequality sign.

These rules tell us when two inequalities are equivalent ( means “is equivalent to”).

In these rules, the symbols A, B, and C stand for real numbers or algebraic expressions.

Slide 9

Solving Inequalities

Here, we state the rules for inequalities involving the symbol ≤.

However, they apply to all four inequality symbols.

Slide 10

Solving Inequalities

Pay special attention to Rules 3 and 4.

Rule 3 says that we can multiply (or divide) each side of an inequality by a positive number.

However, Rule 4 says that, if we multiply each side of an inequality by a negative number, then we reverse the direction of the inequality.

Slide 11

Solving Inequalities

For example, if we start with the inequality

3 < 5

and multiply by 2, we get: